전기방사 조건에 따른 PVDF 방사의 전기장 분포 해석

1. 서 론

대한민국 초미세먼지 현황을 연도별로 살펴보면 2006년부터 초미세먼지 농도가 하락하다가 2008년부터 높아졌으며, 2016년부터는 뚜렷한 하향세를 보이고 있다. 이러한 한국의 초미세먼지농도는 통계적으로 볼 때 악화되기보다는 개선되고 있는 상황이나 2017년 기준 초미세먼지(PM2.5) 농도는 25.1μg/m³으로 여전히 OECD 전체(12.5μg/m³)에 비해 두 배 이상 높은 실정이다. 이는 WHO 권고치 10μg/m³ 보다 높고 정부가 목표한 15μg/m³보다도 높다. 이로 인해 공기청정기, 필터 제조기술 수요가 증가하면서 필터용 나노섬유를 전기방사 방법을 이용한 대량생산이 각광받고 있는 상황이다^[1-3].

전기방사 방법은 전기적인 방법을 이용해 중합체 용액을 분사하여 대전된 여러 가닥의 실 또는 수 마이크론 미터 직경의 나노 섬유를 제조하는 방법이며, 다양한 종류의 나노섬유 제조가 가능하고 제조비용이 저렴하다는 장점이 있다. 하지만 전기방사의 기본적인 형태로 알려진 싱글 노즐(Single Nozzle) 방사 방법은 대량생산이 어렵고 생산속도가 느리다는 한계점을 가지고 있다. 이러한 한계를 극복하기 위해서 멀티 노즐(Multi Nozzle) 방사 방법이 발전되었다. 멀티 노즐 방사 방법은 여러 개의 노즐을 사용하기 때문에 방사되는 용액의 양이 증가하여, 생산 속도가 증가하지만 노즐 사이에서 전기장의 간섭이 일어나 섬유의 직경과 형상이 불균일하거나 전기방사 자체의 테일러콘(Taylor-Cone)형성에 영향을 끼칠 수 있다^[4-7].

본 연구에서는 열적 안정성을 가지며, 여러 필터 또는 멤브레인에 널리 사용되는 PVDF 소재를 방충망에 방사하는 실험적 결과치를 바탕으로 전기방사의 노즐의 Tip 사이즈, TCD(Tip to Collector Distance) 거리 및 전압에 따른 전기장 해석과 전기장 값의 경향을 도출하고 멀티 노즐 일 경우의 Tip 간의 거리에 따른 전기장 값 영향과 방충망 크기(800mm×1500mm)에 방사했을 경우의 전기장 값의 영향에 대한 추가적인 해석을 통해 실제 멀티 노즐을 적용한 전기방사 장치의 노즐 설계와 전기방사 성능에 대한 예측이 가능하도록 데이터베이스를 제시하고자 한다^[8].

2. 전기장 이론

가우스 법칙(Gauss’s Law)은 전기장의 발생과 변화를 다루는 맥스웰의 방정식(Maxwell’s Equation) 중 하나로, 전기장의 발생과 전하의 분포를 연결 짓는 중요한 원리이며, 이는 식 (1)과 같다.

$\nabla \cdot \overrightarrow{E}$는 전기장 $\overrightarrow{E}$의 발산을 나타내며, ρ는 전하밀도, ε₀는 자유공간의 유전상수를 의미한다. 가우스 법칙은 전기장이 전하로부터 발생하는 것을 나타내는데, 전기장 벡터 $\overrightarrow{E}$이 발산은 전하 밀도 ρ에 비례하게 된다. 이 법칙은 특정 폐곡면을 둘러싼 전기장의 총 발산은 그 폐곡면 내에 포함된 전하의 양과 관련이 있음을 나타낸다^[9,10].

또한, 가우스 전하 보존 법칙(Gauss's law for charge conservation)은 전하 보존에 의해 다음과 같이 식(2), (3)과 같이 계산된다.

여기서 E는 전기장 강도를 나타내고, V는 전압 또는 전위를 의미하며, D는 전기 플럭스 밀도, ε_o은 진공의 유전상수, ε_r은 상대유전상수이며, ρ_v는 전하 밀도이다^[9,10].

이중 전기 플럭스 밀도(Electric Flux Density)는 정기장에 관한 개념으로 전기장이 폐곡면을 통과하는 양을 나타내고 단위 면적당 전기 플럭스의 양을 나타내며, 식(4)와 같이 표현된다.

이러한 전하 보존의 원리는 전기적인 시스템에서 전하가 어떻게 동작하는지를 설명하는 중요한 원리이며, 전기장이 공간 내에서 어떻게 분포하는지를 이해하는 중요한 법칙이다^[9,10].

3. 전기장해석의 경계조건 및 해석방법

본 연구에서 수행한 전기장 해석프로그램은 Comsol Multiphysics 6.0이며 AC/DC 모듈을 사용하였으며, 해당 내용은 실제 용액을 방사하는 조건이 아닌 전기 방사 장치의 공간장 내의 전기장의 분포 및 해당값에 대한 결과도출 이므로 정상상태 해석(Steady State Analysis) 조건으로 진행하였다^[11].

3.1 모델링 및 물성치

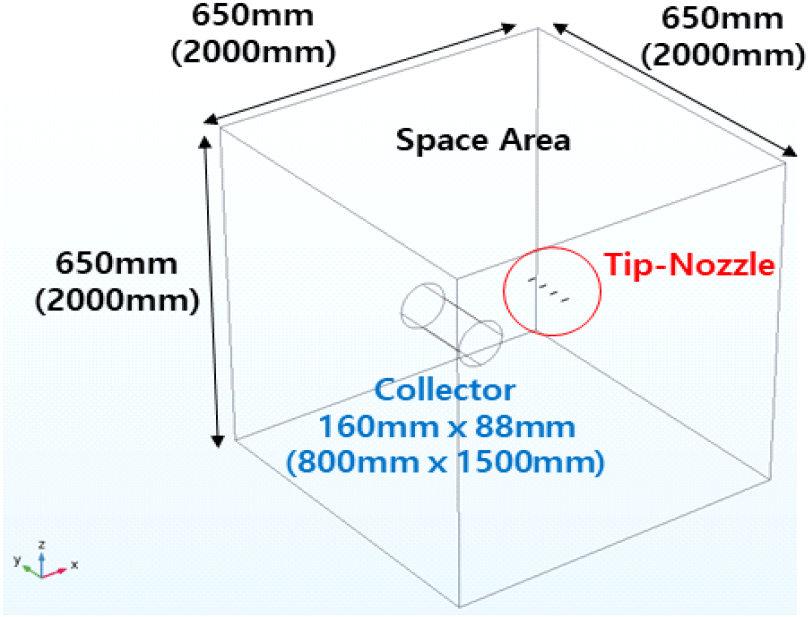
싱글 노즐의 직경, 인가전압, TCD 거리에 따른 해석과 멀티 노즐에서 Tip간 거리에 따른 해석의 경우 Fig. 1에 표현한 전기방사장치를 바탕으로 공간장은 650mm×650mm×650mm, Collector는 160mm×80mm 원기둥 형태로 모델링 하였으며, 실제 방충망 크기를 Collector에 적용하여 노즐의 개수에 따른 전기장 해석의 경우 공간장은 2000mm×2000mm×2000mm, Collector는 800mm×1500mm으로 모델링 하였다.

그림 1. | Fig. 1. 모델링에 사용된 전기방사장치 | Electrospinning device used in modeling

Download Original Figure

그림 2. | Fig. 2. 전기장 해석용 전기방사장치 3D 모델링 | Electrospinning device 3D modeling for electric field analysis

Download Original Figure

또한, 적용하고자 하는 Tip의 경우 길이는 13mm로 일정하며, Table 1과 같이 내/외경 치수를 표현하였으며, 물성치의 경우 실제 모델을 반영하여 공간장은 Air, Tip은 Stainless Steel, Collector는 Aluminum으로 설정하였다.

표 1. | Table 1. Tip별 내/외경 치수 | Inner/Outer Diameter dimensions for each tip

	15G	17G	18G	21G	23G	25G
Outer Diameter (mm)	1.83	1.47	1.24	0.81	0.63	0.51
Inner Diameter (mm)	1.53	1.17	0.96	0.56	0.39	0.30

Download Excel Table

3.2 해석방법

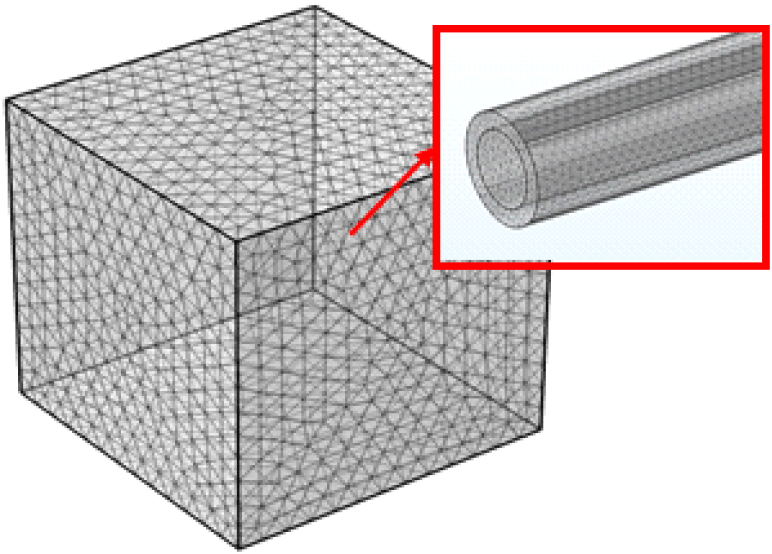
앞서 제시한 3가지 타입의 공간은 Tetrahedra Mesh 형태로 격자를 생성하였으며, 각각의 Mesh 수는 단일 노즐 모델 160,571개, Tip 별 거리에 따른 모델 464,664개, 방충망에 적용하는 모델 4,924,947개이다^[11].

그림 3. | Fig. 3. 해석을 위한 격자생성 | Grid generation for analysis

Download Original Figure

또한, 전기방사에서 고려되는 변수인 온도와 습도는 전기장 장체의 영향이 미비하여 설정하지 않았으며, 실제로 PVDF를 방사하는 형태의 해석이 아니므로 용액의 농도, 점도, 전도도, 분자량, 표면장력에 대한 물성값과 공정변수 중 토출량과 유속에 대한 설정은 하지 않았다^[3].

따라서, 1차적으로 싱글노즐에 대한 해석의 경우 Tip의 사이즈(15G, 17G, 18G, 21G, 23G, 25G), TCD거리(110mm, 130mm, 150mm, 170mm, 190mm), 전압인가량(11kV, 13kV, 15kV, 17kV, 19kV)의 변수를 주었으며, 변수가 다양하고 실제 실험결과를 어느 정도 반영하여 Tip사이즈에 따른 전기장 해석은 전압인가량 15kV, TCD 150mm, TCD거리에 따른 해석은 Tip 21G 사용, 전압인가량 15kV, 전압인가량에 따른 해석은 Tip 21G 사용, TCD 150mm로 설정하였다.

또한, Tip 간 거리에 따른 해석의 경우 Tip을 4개로 설정하고 Tip 21G 사용, 전압인가량 15kV, TCD 150mm로 설정하였으며, 각 Tip 간의 거리는 1cm, 3cm, 5cm로 정하였다.

마지막으로 방충망 사이즈에 적용하는 3번째 해석의 경우 위와 동일한 조건으로 Tip의 개수를 4개(간격 200mm), 8개(간격 100mm), 16개(간격 50mm) 적용하는 방식으로 해석을 진행하였다.

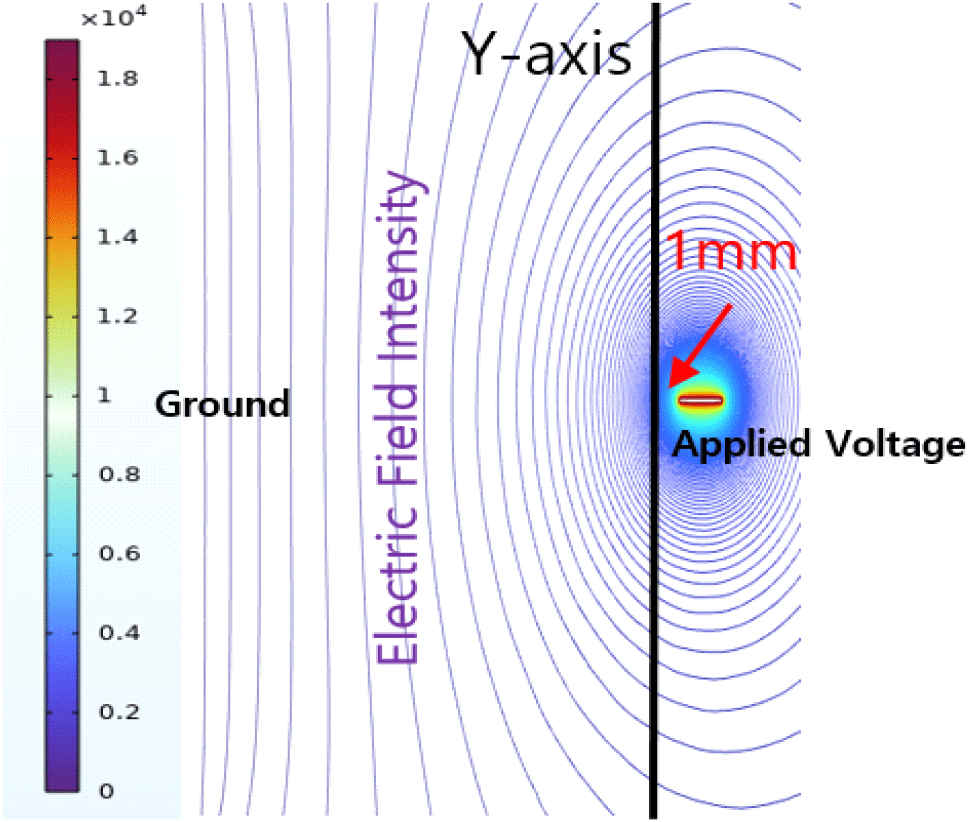
경계조건의 경우 Tip에 전압을 인가하고 Collector에 Ground 조건을 설정하였으며, 해석 결과 도출의 경우 Tip과 Collector의 방사 중심선에 해당하는 xy평면의 중심을 추출하였고 전기방사의 경우 입자나 물체에 전하를 인가하여 이에 따른 운동이나 방사현상이 발생하는 원리로써 Fig. 4와 같이 Tip의 바로 앞쪽에서 Taylor-Cone 등을 형성하여 해당 현상이 발생하므로 Tip앞쪽 1mm y축 선도에 대한 결과를 도출하였다^[11].

그림 4. | Fig. 4. 전기방사의 테일러콘 형성 | Taylor cone formation in electrospinning

Download Original Figure

그림 5. | Fig. 5. 전기장 해석의 경계조건 | Boundary conditions for electric field analysis

Download Original Figure

4. 전기장해석의 결과 및 고찰

4.1 공정변수에 따른 싱글노즐의 전기장 해석 결과

공정변수에 따른 싱글노즐의 전기장 해석을 진행하였으며, 첫 번째로 노즐 타입별 전기장 세기의 경우 직경이 감소할수록 점차적으로 전기장 값이 감소하는 것을 확인할 수 있다.

15G의 경우 35.47kV/cm이며, 가장 직경이 작은 25G의 경우 27.39kV/cm으로서 약 8.08kV/cm의 전기장 세기의 감소를 보였으며, 이는 동일한 전압이 인가되었을 경우더라도 인가되는 대상체의 부피와 표면적 감소에 따른 영향으로 판단된다.

그림 6. | Fig. 6. 싱글노즐에 대한 전기장 해석의 결과 | Results of electric field analysis for single nozzle

Download Original Figure

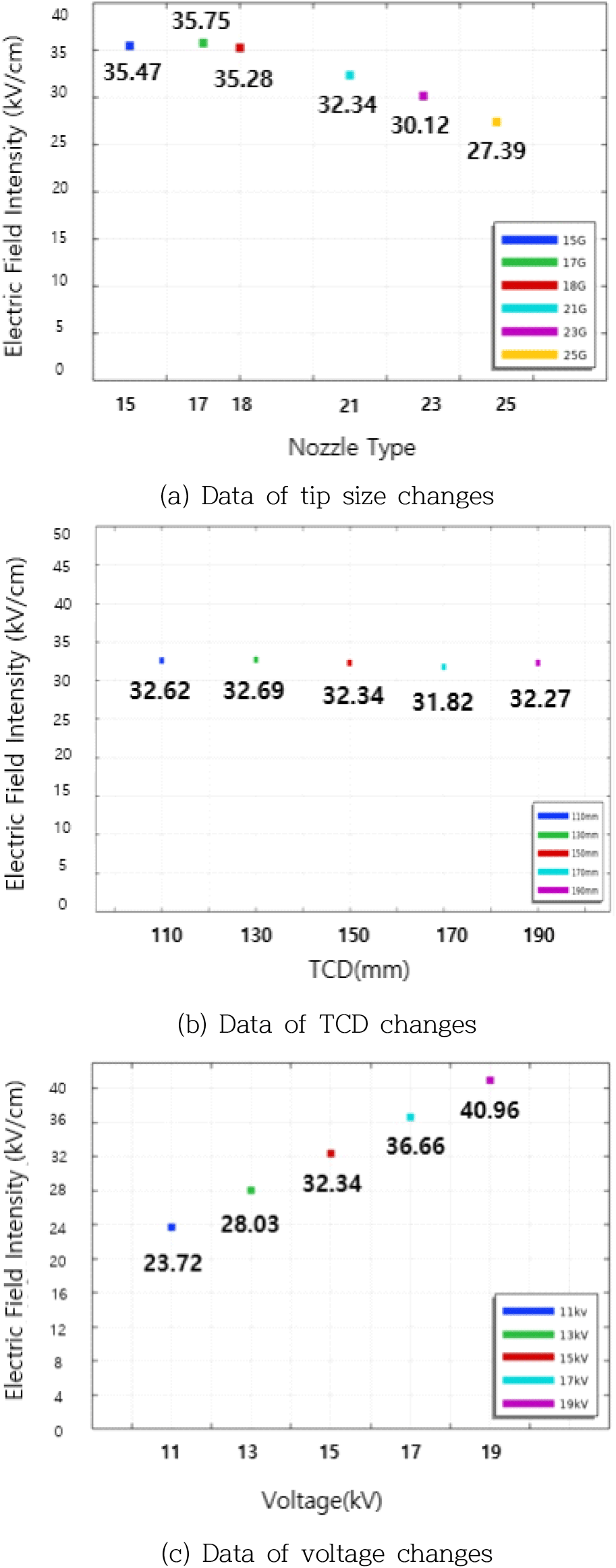
TCD의 거리에 따른 전기장 세기의 경우 TCD 거리가 130mm일 경우가 32.69kV/cm로 가장 높고 170mm인 경우가 31.82kV/cm로 가장 낮게 나왔으며, 전체 5가지의 변수 모두 값의 큰 차이를 보이지 않아 TCD 거리에 따라 전압이 인가되는 대상체와 Ground 사이의 거리는 Tip근처의 전기장 분포에 큰 영향을 끼치지 않는 것으로 판단된다.

마지막으로 전압에 따른 전기장세기의 결과의 경우 11kV가 23.72kV/cm이고 점차적으로 증가하여 19kV의 경우 40.96kV/cm으로 큰 차이를 보였으며, 이는 앞서 이론에서 언급한 전기장세기와 전압의 비례관계를 통한 예상된 결과를 보였다^[3].

전기방사의 경우 방사체의 물성, 형태, 크기 등에 의한 영향에 따라 적절한 전기방사 조건이 필요하며, 전기장 세기가 강하다고 해서 반드시 방사 자체가 원활하게 이루어지는 것은 아니고 특정 임계값이 존재한다. 따라서, 이러한 결과를 통해 멀티노즐에 따른 전기장세기 변화를 분석하고자 Tip 21G 사용, TCD 150mm, 전압인가량 15kV를 기준으로 설정하였다.

4.2 멀티노즐 Tip간 거리에 따른 전기장 해석 결과

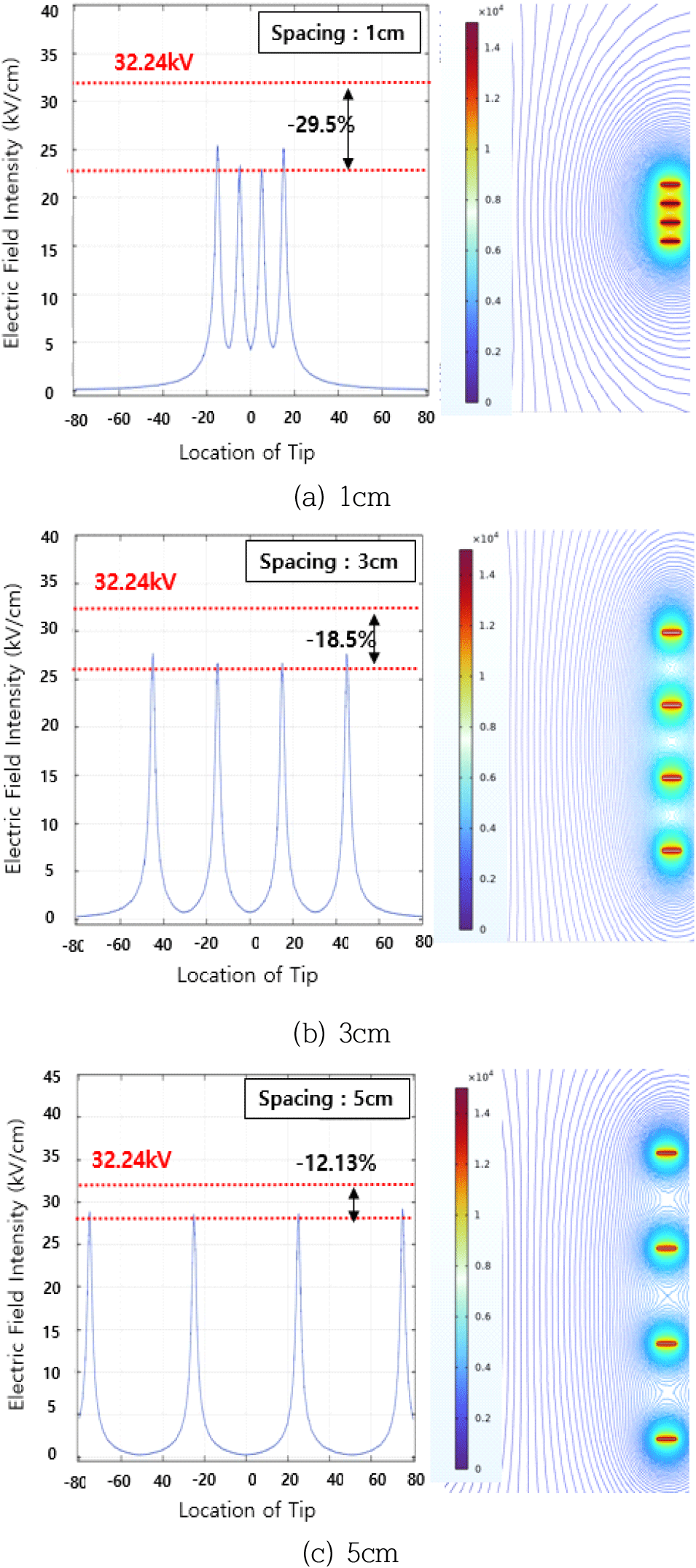
Tip과 Tip사이의 거리 변화에 따른 전기장 세기에 대한 해석결과, 앞서 4.1절에서 도출한 전기장 세기값 32.34kV/cm(21G, TCD150mm, 15kV)을 기준으로 1cm의 경우 최고 25.26kV/cm(−22.9%), 최소 22.80kV/cm(−29.5%)의 값을 보였고 3cm의 경우 최고 27.41kV/cm(−15.25%), 최소 26.36kV/cm(−18.5%), 5cm의 경우 최고 28.94kV/cm(−11.5%), 최소 28.42kV/cm(−12.13%)의 전기장세기 결과값을 나타냈다.

이를 통해 Tip간의 거리가 가까울수록 전기장의 간섭이 발생하는 것으로 확인할 수 있었으며, 이는 양쪽에 Tip을 두고 있는 중앙의 2개의 Tip에서 더 큰 영향을 끼치는 것을 알 수 있으며, Contour를 통해서도 이를 구분할 수 있다.

그림 7. | Fig. 7. Tip간의 거리에 따른 전기장세기 및 Contour | Electric field Intensity and contour lines according to the distance between tips

Download Original Figure

4.3 Collector에 실제 방충망크기를 적용한 멀티노즐 전기방사장치 Tip개수에 따른 전기장 해석 결과

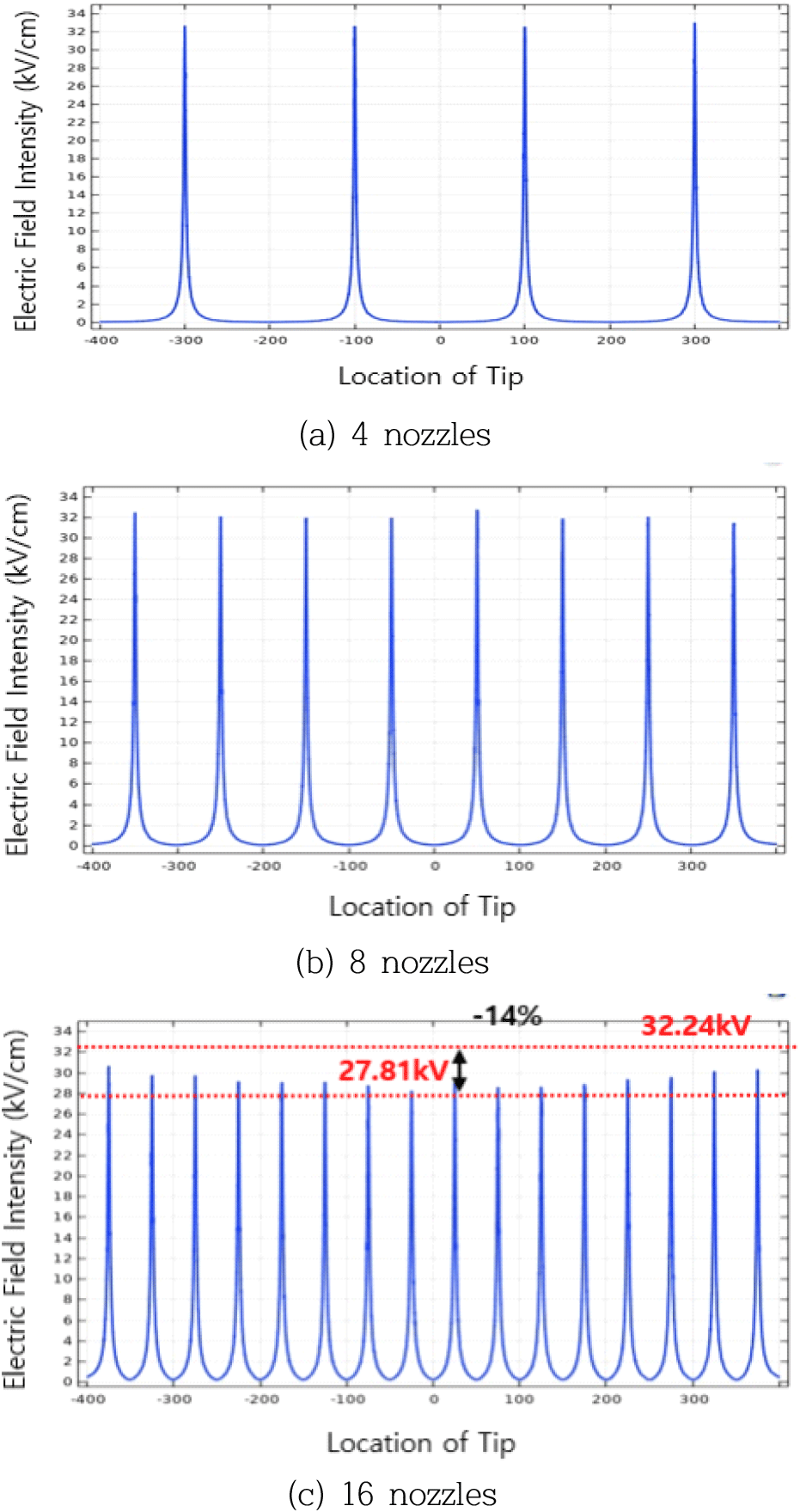
Tip개수에 따른 실제 방충망 사이즈의 Collector에 적용한 해석결과, 앞서 4.1절에서 도출한 전기장 세기값 32.34kV/cm(21G, TCD150mm, 15kV)을 기준으로 노즐 4개의 경우 최고 32.97kV/cm(+0.19%) , 최소 32.40kV/cm(+0.02%)의 값을 보였다.

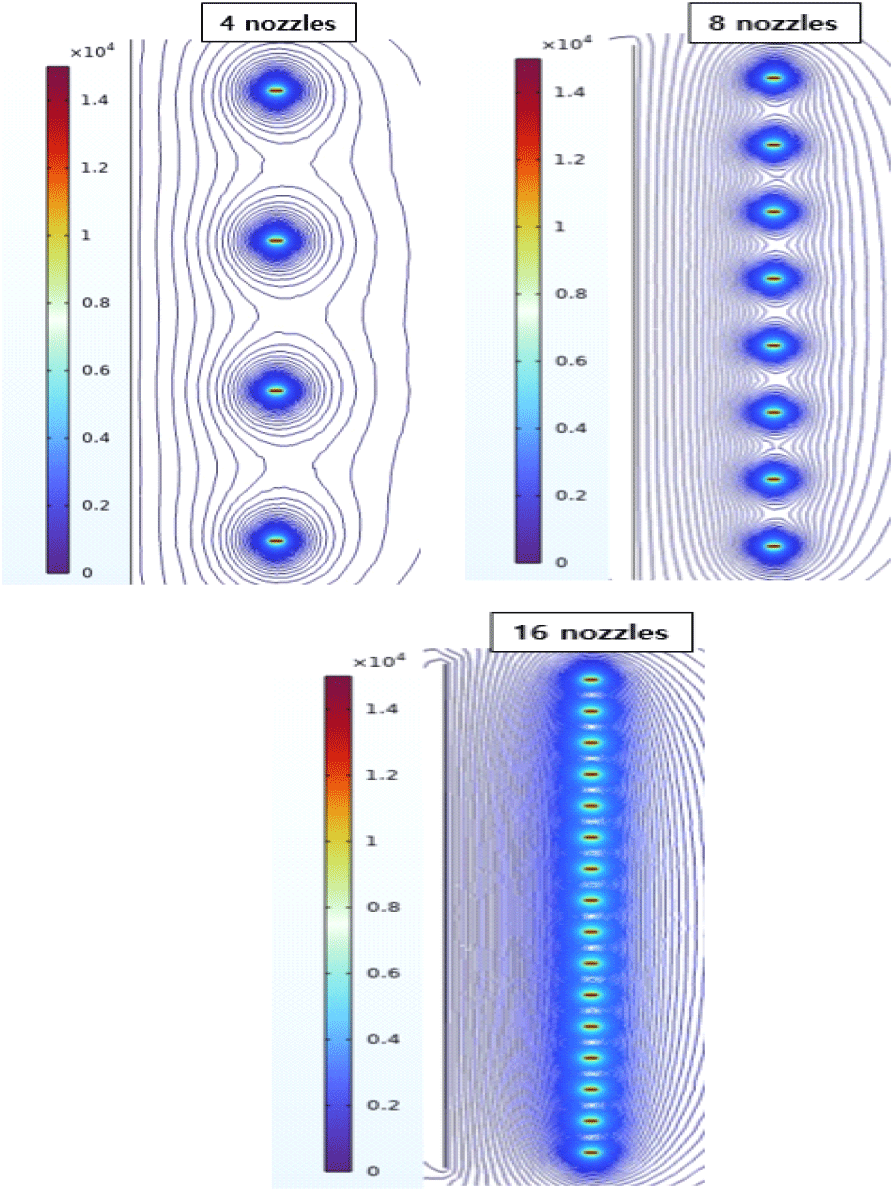
또한, 8개의 노즐의 경우 최고 32.29kV/cm(−0.16%) , 최소 31.21kV/cm(−3.5%)의 값을 보였으며, 16개 노즐의 경우 최고 30.61kV/cm(−5.4%) , 최소 27.81kV/cm(−14%)의 값을 나타냈다.

이를 통해 노즐이 4개인 경우와 8개인 경우 사이 간격이 100mm 이상으로서 는 싱글노즐로 방사할 경우와 팁 간의 사이 전기장간섭이 미미한 것으로 나타났으나 노즐이 16개인 경우는 앞서 4.2절의 결과와 유사한 패턴으로서 간섭 발생을 통해 본 논문에서 방사 임계값으로 설정한 전기장세기에 한참 미치지 못한 결과를 보였으며, 이는 원활한 전기방사 결과를 기대하기 어려울 것으로 판단된다.

따라서, 실제 실험을 통한 Collector의 방사면적을 확인함으로써 이러한 해석 결과와 비교하여 Nozzle 간의 개수, 즉 멀티노즐 간의 사이 간격을 설계함으로써 공정라인의 단순화 및 단가를 최소화할 수 있는 방법을 파악하고 멀티노즐을 통한 원활한 전기 방사를 진행함으로써 생산속도 증가를 기대할 수 있을 것으로 판단된다.

그림 8. | Fig. 8. 노즐 개수에 따른 전기장 세기의 결과값 | Results of electric field intensity according to the number of nozzles

Download Original Figure

그림 9. | Fig. 9. 노즐 개수에 따른 전기장 세기의 Contour 결과 | Contour lines according to the number of nozzles

Download Original Figure

4. 결 론

본 연구에서는 방충망 필터링 효과를 증가시키기 위한 PVDF 나노섬유를 전기방사하는 방식을 적용하고자 전기방사 장치의 설계에 대한 예비단계의 일환으로 전기장 해석을 타입별 진행한 내용이다.

싱글노즐을 이용한 전기방사 해석의 경우 Tip의 사이즈가 감소할수록 전기장 세기의 감소를 보였으며, 이는 동일한 전압이 인가되었을 경우더라도 인가되는 대상체의 크기 감소에 따른 영향으로 판단하였으며, TCD 거리에 따른 전기장해석의 경우 전압이 인가되는 대상체와 Ground 사이의 거리는 Tip 근처의 전기장 분포에 큰 영향을 끼치지 않는 것으로 보이며, 인가전압에 따른 해서의 경우 이론에서 언급한 전기장세기와 전압의 비례관계를 통한 예상된 결과를 보였다.

멀티노즐의 Tip간의 거리에 따른 전기장 해석의 경우 본 논문에서 기준으로 정한 32.34kV/cm(21G, TCD150mm, 15kV)과 비교하여 1cm의 경우 22.80kV/cm(−29.5%), 3cm의 경우 26.36kV/cm(−18.5%), 5cm의 경우 28.42kV/cm(−12.13%)의 전기장세기 결과값을 나타냈다.

이를 통해 Tip 간의 거리가 가까울수록 전기장의 간섭이 발생하는 것으로 확인할 수 있었으며, 이는 양쪽에 Tip을 두고 있는 중앙의 2개의 Tip에서 더 큰 영향을 끼치는 것을 알 수 있었다.

Tip개수에 따른 실제 방충망 사이즈의 Collector에 적용한 해석의 경우 4개의 노즐과 8개의 노즐을 사용하였을 경우 싱글노즐인 경우와 거의 같은 값을 나타내었으며, Tip간의 거리가 100mm 이상일 경우에는 해당조건에서 전기장간섭이 미미한 것으로 나타났으나 노즐이 16개인 경우는 방사 임계값으로 설정한 전기장세기에 한참 미치지 못한 결과(27.81kV/cm(−14%))를 보였으며, 이는 원활한 전기방사 결과를 기대하기 어려울 것으로 판단된다.

따라서, 이러한 해석적 결과를 바탕으로 실제 실험을 통해 Collector의 방사면적을 확인하고 Nozzle 간의 개수, 즉 멀티노즐 간의 사이 간격을 설계함으로써 공정라인의 단순화 및 단가를 최소화할 수 있는 방법을 파악하고 멀티노즐을 통한 원활한 전기 방사를 진행함으로써 생산속도 증가를 기대할 수 있을 것으로 판단된다.