변형량이 큰 유연보의 진동특성 이론해석

비성형 보의 지배 방정식을 구하는 대상 모델은 다음 그림과 같이 수직 방향의 외팔보(의 형태를 갖으며, 비선형 보를 가진 시키는 방법은 밑에서 수평방향으로 이동시키는 것이다. 운동방정식을 유도하는 데에 있어서, 보의 두께가 길이에 비하여 대단히 작아서 전단변형과 보의 회전 관성량을 무시하는 가정을 적용하였다. 또한 보의 횡 방향 진동 크기가 시스템의 주요한 사항이므로, 보의 축 방향 공진 현상 또한 무시하였다. 이것은 보의 축 방향의 공진이 굽힘 방향의 공진 주파수 보다 매우 높은 주파수 대역의 성분을 갖고 있을 것으로 생각되기 때문인 점도 고려되었고, 같은 이유로 보의 토숀에 의한 변형 주파수도 무시되었다. 가진에 의한 변위가 매우 큰 비선형 보의 운동 방정식을 산출하기 위하여 Euler Bernoulli 이론을 이용하였다. 그림1 에서 ‘s’점에서 작용하는 굽힘 모멘트는 구하면

E: Youngs Modulus

I: Cross Sectional Moment of Inertia

k(s): radius of curvature at section

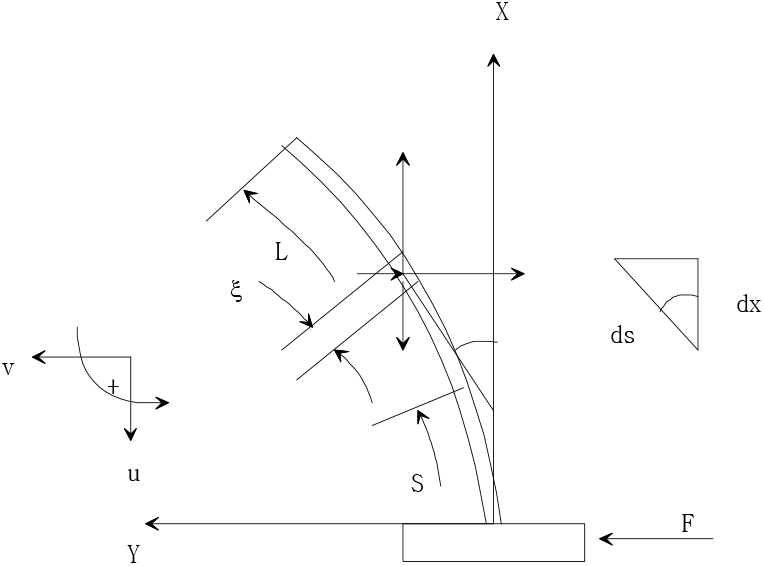
이 되고, 식(2-1)에서 정의된 변수는 이다. 곡률 반경 함수와 보의 굽힘각의 관계를 구하면

이 되고, 이때 는 임이 위치 의 굽힘 각의 기울기 이다. 식(2-2)에서 정의된 의 미분 항을 구하면,

where s^* = s/L, v^*=v/r, $t*=\frac{1}{L^3}\sqrt{\frac{EI}{\rho A}t}$

r: radius of gyration for the cross sectional area

K: stiffness of beam

cf: eq. (10) is dropped with the *

이 되고, 이것을 이용하여 식(2-1)에서 표시된 모멘트 방정식을 구하면,

이 된다. 식(2-4)는 보의 임의 점 에 작용되는 모멘트를 표시하는 것이데, 이식은 다음과 같은 두 가지의 모멘트 성분의 합 즉 수직 관성량 (lateral inertia)와 및 수평방향 관성량 (longitudinal inertia)의 원인으로 발생하는 외부 모멘트(external moment)으로 표현이 가능하다.

이러한 두 가지의 모멘트 성분을 적분으로 표현하면

이 되고, 이때의 축 방향의 변위는

로 정의되며, 축 방향 변위 가속도 성분, 즉 변위를 두 번 미분 한 값을 기구학적 조건을 이용하여 표현하면 다음과 같다.

이 식들을 Euler-Bernoulli의 이론에 적용하여 보의 운동 방정식을 무 차원 수로 정리 하면 다음과 같다.

단 여기서 정의된 변수는 다음과 같다.

식 (2-10)의 비선형보의 운동방정식은 진동에 의한 보의 매우 큰 비선형 보의 운동을 해석하기 위한 운동방정식으로, 이러한 비선형 식을 풀기 위하여 시간에 변화에 따른 가중치를 분리한 비선형 해를 구하는 방법인 ‘method of multiple scale’^[3]을 활용하여 해석한다. 제시된 비선형 방정식의 항이 3차 항인 ‘cubic term’으로 되어 있으므로, 응답해 v(s,t)를 다음과 같이 표현할 수 있다.

단, 여기서 표현된 가중치가 포함된 시간 변수는 다음과 같이 정의 된다.

식(2-12)를 식(2-10)에 대입하고 외팔보의 경계조건을 고려하여 1차 항을 정리하면 다음과 같이 표현된다.

단 여기서 변위‘’는 식(2-11)에서 표현된 ‘’의 ‘’를 생략하여 표시한 것이다. 3차 항 역시 지배 방정식과 경계조건을 정리하면 다음과 같다.

단, 여기서 표현된 변수는 다음과 같이 정의된다.

보의 지배방정식에 대하여 변수 분리법에 의하여 해를 구하기 위하여 보의 응답 해를 모우드 함수와 시간에 따른 함수의 조합으로 다음과 같이 정의할 수 있겠다.

식(2-14)는 일반적인 선형 보의 운동방정식으로써 1차 항의 응답은 전형적인 선형 해를 구하는 방법으로 산출할 수 있다. 모우드 함수 를 정의하여 보의 응답 해를 표현하면 다음과 같은 결과를 얻게 된다.

여기서 시간의 함수를 ‘G_i(t)=cos(ω_it+β)’의 조화 함수로 가정하면 식(2-14)의 모우드 함수는 다음과 같이 표현되고

이때, 미분 방정식의 계수는 보의 물리량으로 다음과 같이 정의 된다.

모우드 해를 구하기 위하여, 함수 ϕ_i(s) 를 다음과 같이 가정하면,

where, ϕ_i(s):solution for mof eq.(18)

ω_i=natural frequence of beam

이 되고, (2-20)식에 경계조건을 적용하면

이 된다. 이때’z’의 고유치는 다음의 방정식(2-22)를 만족한다.

식(2-22)의 고유치를 구하기 위하여 특성방정식을 정의하면 다음과 같이 표현되고

식(2-23)의 고유치는 다음 조건을 만족 하게 된다.

식(2-24)의 처음 3개의 근을 수치해석 기법인 ‘Newton Relphson’의 방법을 이용하여 구하면, z=1.8751, 4.6941, 7.8547 이 된다. 고유벡터(eigen vector)는 보의 경계조건과 식(2-20)을 이용하여 구하게 되는데, 이러한 조건을 정리하면 다음식 (2-25)으로 정리 된다.

where ${\displaystyle {\int }_0^1{\varphi }_i^2(s)ds=1}$

식(2-25)에서 정의된 식은 보의 모우드 형태 (mode shape)을 결정해 주는 식이며, 식(2-24)에서 산출된 고유치로 표현되는 보의 고유 진동수(natural frequency)는 다음과 같이 표현된다.

식(16)의 시간에 대한 비선형 항의 해를 구하기 위하여 Galerkin Method를 사용하여 보자. 비선형 해를 적용하기 위하여 응답함수를 다음과 같이 가정하면, 1차 항은

이 되고, 4차 항 은

으로 표현된다. 식(27),(28)을 식(15)에 대입하여 정리하면, 비선형 특성이 고려된 지배 반정식은

이다. 단, 여기서 표현된 변수 ‘α₁, α₂, α₃, ’은 다음과 같다.

선형화된 보의 고유진동수와 유사하게 가진 시켰을 때의 응답을 구하여 본다. 가진 주파수는 다음과 같이 표현할 수 있고

식(2-28)을 식(2-27)에 대입하고 해의 해석조건을 구하면 다음과 같다. 비선형 시스템의 해의 해석 조건은 비선형 진동계의 응답 해가 존재하는 조건을 의미한다.

where

식(2-31)을 풀어 실수 부와 허수 부를 분리하여 정리하면 다음과 같다.

그리하여 1차 응답함수는 다음과 같이 표현된다.

안정조건은 만족하는 a, γ는 식(2-31)으로부터 식(2-35)와 같음 조건을 만족하게 된다.

또한 위상 및 변위에 관한 관계는 식(2-35)를 식(2-33)에 대입하여 정리하면 다음의 식(36)와 같은 식으로 표현 된다.

식(2-36)는 진폭과 가진 위상과의 관계로 안정화 조건을 보여주는 식으로써 위상 변화에 따른 진폭크기를 나타내준다. 즉 식(2-34)의 진동 응답은 해의 존재를 만족하며, 진동계의 안정 조건을 만족하는 식(2-35)과 식(2-36)를 만족하는 범위에서 존재하게 된다.

가진력에 의한 변위가 매우 큰 비선형 보의 변위의 크기는 계의 고유 진동수에 영향을 미치게 된다. 특히 이러한 유연한 구조물에 대한 정밀한 제어를 할 경우에는 이러한 물리적인 현상에 대한 이해가 매우 중요하게 된다.

가진력에 의한 변위가 매우 큰 유연 구조물의 과 댐핑 영향을 무시하였을때의 고유 진동수의 변화에 대하여 알아보자. 식(2-31)로부터

을 만족한 조건에서, 식(2-35)를 식(2-33)에 대입하여 정리하면 다음과 같은 식을 얻게 된다.

식(2-36-a)에서 a는 상수임을 의미하고, 식(36-b)를 정리하면 다음과 같다.

식(2-37)에서 의미하는 바는 비선형 현상에 의한 고유진동수의 변화량은 식(2-30)에서 정의된 α₁, α₂, α₃,’ 즉 변위의 크기가 반영된 항과 선형 시스템의 고유진동수 ‘ω_n’에 영향을 받음을 알 수 있다. 매우 유연한 비선형 보의 고유 진동수는 결국 선형 고유진동수에 식(2-37)에서 산출된 비선형 영향에 의한 변화 량을 더하여 산출되므로, 식(2-16), (2-37)으로부터 비선형 보의 변화된 고유진동수는

이다. 식(2-38)은 비선형 진동계의 진폭에 따른 고유진동수의 변화를 표시하는 식이다. 진폭의 크기가 증가할수록 고유진동수의 크기는 감소하게된다.