1. 서 론
육군은 미래 첨단과학기술이 구현된 지상전투체계 Army TIGER 4.0을 추진 중이다. Army TIGER 4.0 체계는 개별 전투체계에 대한 운용개념이나 기술적 발전에 한정하지 않고 제대별 전투개념, 부대구조 및 전력구조까지 종합적으로 반영된 미래 육군의 청사진과도 같다. Army Tiger 4.0 체계의 추진 배경[1]은 다음과 같다. 첫째, 육군의 부대 감소 및 장병의 복무기간 단축과 더불어, 육군의 현 무기체계들이 2.5세대 수준의 머물러 있기 때문에, 해·공군의 첨단 무기체계와의 효과적인 합동성 발휘를 위해서는 발전된 수준의 체계들이 육군에 전력화될 필요성하다는 것이다. 둘째, 핵과 대량살상무기(Weapons of Mass Destruction, WMD) 등으로 위협 자산을 지속 고도화 중인 북한과 동북아 강대국들의 이권 추구 등으로 한반도의 전략환경은 어느 때보다도 불확실성이 고조되고 있다. 셋째, 미국, 러시아, 중국, 이스라엘 등 군사 선진국들은 여단 현대화 프로젝트 등으로 군사혁신을 추진 중이다. 넷째, 과학기술 발전에 따른 무인화 및 인공지능 기반의 무기체계 활용 증대가 급격한 미래 전장환경의 변화를 가져올 것이다.
육군의 Army TIGER 4.0 체계는 드론봇 전투체계 및 워리어플랫폼을 포함하는 3대 전투체계를 포함한다[2]. 이 체계는 AI(Artificial Intelligence) 기반 초연결 지상전투체계를 중심으로 발전되고 있으며, 기동화, 지능화, 네트워크화를 핵심개념으로 한다. 기동화는 전 제대의 기동수단 확보를 위해 기동 플랫폼에 타 임무장비 혹은 전투체계를 결합하는 것으로 드론봇이 장착된 차륜형장갑차 혹은 소형 전술차량 등으로 기동화 추진이 가능하다. 지능화는 AI 기반 초지능 의사결정체계로 상황판단 및 결심 지원 체계를 구축하는 것으로, 기반 C4I (Command, Control, Communication, and Intelligence) 체계를 구축하거나 유·무인 복합체계에 의한 전투수행을 의미한다. 네트워크화는 전 플랫폼을 초연결하여 통합 네트워크체계를 구축하는 것으로 통신망, 기동수단, 감시 및 타격 수단 등을 실시간 연결하여 전장을 가시화함으로써, 지휘관 혹은 운용자의 즉응적인 의사결정을 지원하여 전장효과 극대화를 이끌어낼 수 있는 요인으로 작용한다.
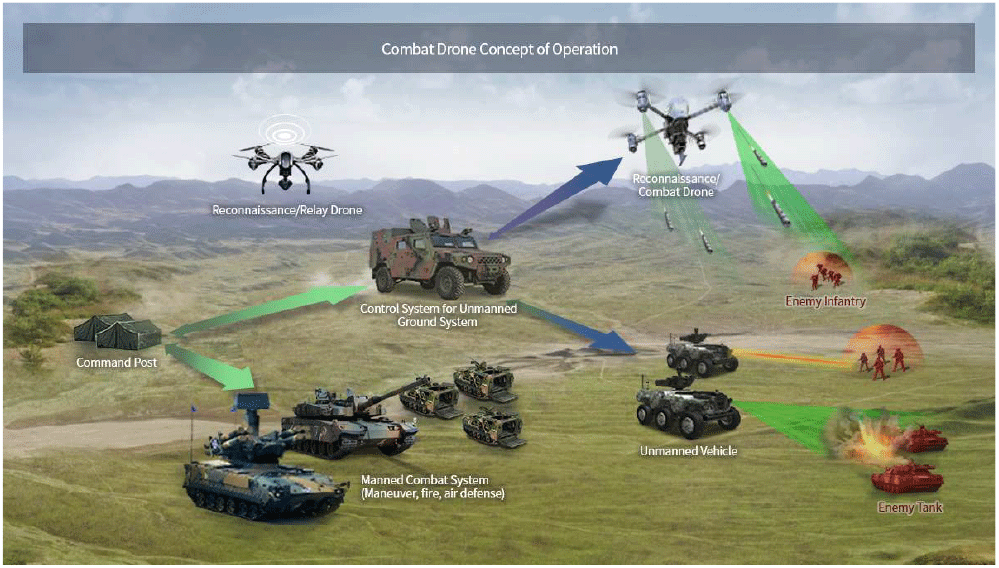
드론봇(dronebot) 전투체계 그림 2와 같이 드론(drone)과 로봇(robot)의 합성어로 전장에서 활용 가능한 무인전투체계를 총괄하는 의미로 사용된다. 그림 3과 같이, 드론봇을 활용한 전투체계의 운용개념은 통상 총 3가지로 구분된다[4]. 첫째, 공중 및 지상 유·무인 체계를 통합 운용하여 월등한 기동력과 적 핵심표적에 대한 감시·타격 능력을 보강한다. 이를 위해, 제대별 정찰드론 및 공격드론을 편제하고 미사일 및 포병화력을 활용할 예정이다. 둘째, 전투원의 희생을 최소화하여 작전목적 달성을 가능하도록 한다. 적 지뢰지대 정찰 및 파괴, 도시지역 지하공동구 감시 및 타격 등 드론봇을 적극 활용하여 인명 피해 최소화를 위해 노력한다. 셋째, 드론과 로봇산업 경쟁력 강화를 위한 주도적 역할을 수행한다. 00건 0만여6) 세트의 드론봇 소요를 창출하고, 상용드론 실증(Test-bed) 및 표준화를 추진하여 4차 산업혁명을 선도하고자 한다.
본 논문에서는 감시/정찰 혹은 공격용 등의 임무를 수행하는 무인체계인 UAV(Unmanned Aerial Vehicle) 및 UGV (Unmanned Ground Vehicle)의 효과적인 지휘통제 및 통신을 위한 Multiplexer 할당문제(Multiplexer Assignment Problem, MAP)를 소개하고, 실제 전장환경에서 즉응적인 해 도출이 가능한 계산시간 면에서 효율적인 해법을 제안하고자 한다. MAP는 다양한 네트워크 환경에서 활용될 수 있는 최적화 모형으로 무인체계 혹은 유·무인체계 협업의 작전환경에서 효율적인 네트워크 구성에 활용될 수 있을 것으로 기대된다. MAP는 네트워크 최적화 문제의 한 유형으로, 각 네트워크 구성요소를 연결하는 가운데 필요자산을 사용을 최소화하거나 효용을 극대화하는 문제이다. 민간에서 가장 흔한 응용분야는 전기 설계 자동화(Electronic Design Automation, EDA) 분야로, EDA는 전기회로의 최적설계와 같이 전기시스템의 설계나 개선의 전 과정을 포함한다. 응용분야인 군사OR(Military Operations Research)에서의 MAP는 군사 상황에서 자원의 최적 배분(optimal allocation)과 직접 연관성이 있으며, 비용을 최소화 하거나 효용성을 최대화하는 등의 목적을 지닌다. MAP 해법에 대한 연구는 몇몇 문헌에서 다루어져 왔다. Sutter et al.[8]의 논문에서는 simulated annealing 기반의 휴리스틱 해법을 제안하였으며, MAP에 대한 수학적 모형 및 소개는 Wolsey[7]의 교재에 제시되어 있다.
본 논문의 2절에서는 MAP의 수학적 모형에 대해 살펴보며, 목적함수와 제약조건의 의미를 상세히 기술하여, 향후 실전적 활용을 위한 응용모형으로의 발전 가능성을 살펴본다. 3절에서는 이웃해 기반 휴리스틱 알고리즘을 제안하고, 여러 실험을 통해 계산 효율성과 정확도 면에서의 본 논문에서 제안하는 해법의 성능을 비교 분석한다. 마지막으로 4절에서는 본 연구의 의의와 향후 연구 방향에 대해 간략히 논의한다.
2. 수학적 모형
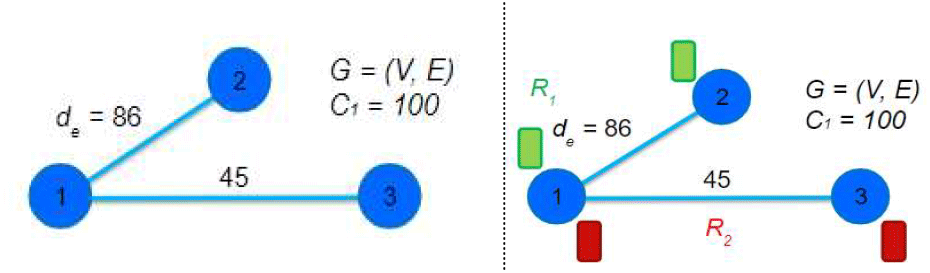
네트워크 상에서 멀티플렉서 할당 예시는 다음과 같다. 그림 4의 네트워크 G=(V, E)는 총 3개의 마디와 두 개의 호로 구성되어 있으며, 각 호의 수요 de 가 표현되어 있다. 고리의 용량이 C1 = 100일 때, 호 (1,2)와 (1,3)는 각각 다른 고리인 R1과 R2에 할당되어야 하며, 이때 사용되는 멀리플렉서의 수는 총 4개(녹색 2개, 적색 2개)이다.
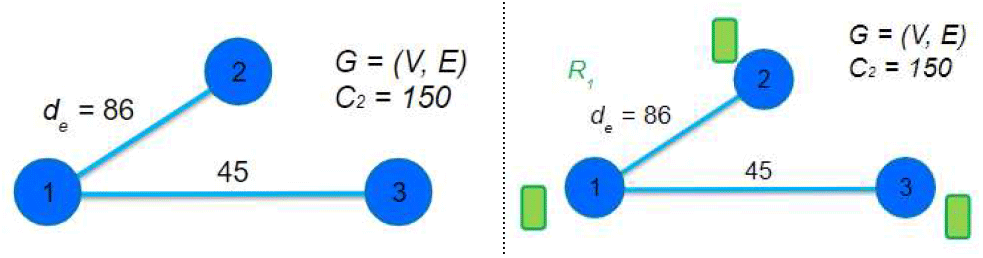
동일한 네트워크 G= (V, E)에 대해, 그림 5와 같이 고리의 용량이 C2 = 150일 때, 호 (1,2)와 (1,3)를 하나의 고리인 R1 에 할당할 수 있으며, 이때 사용되는 멀리플렉서의 수는 총 3개이다.
주어진 네트워크 G=(V, E)의 Multiplexer 할당문제는 다음과 같이 이진정수선형계획법 (Binary Integer Linear Programming, BILP)로 모형화 된다[7].
<인덱스>
k : 고리(ring)의 인덱스,
e ∈ E: 호(edge)의 집합,
i, j ∈ V: 마디(node)의 집합.
<파라미터>
C (> 0) : 고리의 용량,
de (> 0) : 호 e(∈E)의 수요
(communication demand).
<결정변수>
<모형화>
고리(ring)의 인덱스는 k로 표기하되 총 n 개의 고리가 존재할 수 있음을 가정한다. 집합 E 와 V 는 주어진 네트워크 G= (V, E)의 무향호와 마디의 집합을 각각 의미하며, e 는 호의 집합 E 에 속하는 호, i, j 는 마디의 집합 V 에 속하는 마디를의 인덱스를 표현한다. 각 고리의 용량은 균일한(identical) 값인 C, 각 호의 수요를 de 로 표기한다. 이 네트워크 최적화 문제의 결정변수는 마디 i 위치에 고리 k에 대한 multiplexer 설치여부를 표현하는 이며, 마디 i, j 에 고리 k에 대한 multiplexer가 설치되었을 때 (즉, ), 마디 i, j 를 잇는 호 e = (i, j)의 수요 de의 충족여부 표현하는 가 이진결정변수(binary decision variable)로 설정된다.
수학적 모형의 제약식 (2)는 모든 호 e(∈E) 가 반드시 하나의 고리(ring)에 할당되어야 함을 나타내며, 제약식 (3)에 각 고리에 할당된 호의 수요 는 고리의 용량(C)를 초과하지 않아야 한다. 또한, 제약식 (4)-(5)는 호 e = (i,j)의 수요 de 가 고리 k에 할당되기 위해서는 해당 multiplexer가 마디 i, j 에 설치되어야 함을 표현한다. 마지막으로 제약식 (6)-(7)은 결정변수는 0 혹은 1의 값을 갖는 이진변수로 제약된다. 이 모든 제약조건 (2)-(7)을 만족하는 가운데, 목적함수 (1)에 의해 설치된 multiplexer의 수의 합이 최소화되는 할당안을 도출한다.
이외에도, 문제 상황에 따라 목적함수와 제약조건을 일부 수정하여 복잡한 형태의 MAP를 정의할 수도 있다. 예를 들어, 두 종류의 multiplexer가 활용될 수 있는 상황이라면, 몇몇 제약식을 기본모형에 추가해야 한다. 예를 들어, multiplexer Type 1은 용량이 C1이며 각 multiplexer의 비용은 α, multiplexer Type 2는 용량이 C2(>C1)이며 multiplexer의 비용은 β일 때의 상황을 고려해보자. 그렇다면, 기본모형에 다음의 결정변수 와 를 추가하고, 목적함수는 (1)′로 수정하고, 제약식 (8)-(10)을 추가한 응용모형을 활용할 수 있다.
3. 휴리스틱 해법 및 실험
본 논문에서 제안하는 Greedy 휴리스틱 방법은 최적해는 아닐지라도 기존 해에서 순간 가장 효과적인 방향으로 해를 개선해나가는 휴리스틱 방법론 중 하나이다. 본 절에서 제시하는 greedy 휴리스틱은 임의로 선택된 초기해에서 추가 가능한 가장 큰 수요를 가진 인접한 호를 추가해나가는 방식이다. 본 논문의 greedy 휴리스틱 해법(Greedy Heuristic Algorithm, GHA)의 세부적인 절차는 다음과 같다.
Step 0. k = 1.
Step 1. (Choosing initial edge) Start with edge e which has positive demand. If there exist multiple positive edges, choose the smallest index among them.
Step 2. Add e to the ring k.
Step 3. (Finding and adding an adjacent edge) Find an addible edge e with the largest demand among edges which are adjacent edges in ring k. Add edge e in the ring k and set de = 0. Repeat step 3 until there is no edge that can be added to ring k.
Step 4. k = k + 1 and go to step 1 if there exists an edge of positive demand. Otherwise, stop.
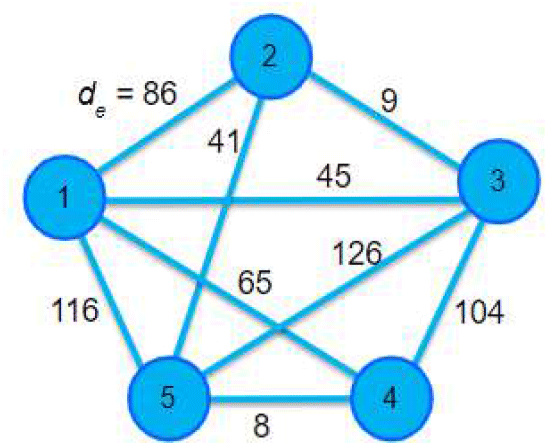
위 Greedy 휴리스틱 알고리즘은 각 반복단계(iterations)별로 하나의 고리(ring)에 초기 할당한 호를 기준으로 인접한 호들을 잔여용량 범위 내에서 새로운 호를 추가하는 방식으로 설계되었다. Step 1은 최초 임의의 호를 하나 선택하는 것으로 시작한다. Step 2에서는 최초 선택한 호를 고리 k에 할당하고, Step 3에서는 최초 할당한 호의 인접 호들 중에서 de 의 값이 가장 큰 호부터 순차적으로 고리 k에 추가한다. 더 이상 k = 1 인 고리에 호를 추가할 수 없게 되면(즉, 고리의 잔여용량이 부족하면), 현재까지 할당한 호들의 수요 de를 0의 값으로 설정하고, 다음 고리 k = 2 로 넘어간다. 이때, k = 1 일 때와 동일하게 Steps 1-3을 반복 적용하며, 이 반복단계(k = 2)에서 다시 고리의 용량 범위에서 호들이 할당될 때까지 반복한다. 해당 알고리즘의 절차를 상세히 보이기 위해, 그림 6의 네트워크 예제에 GHA를 적용한 결과를 표 1에 각 반복단계별로 순차적으로 제시하였다.
| iterations | Results |
|---|---|
| k = 1 Steps 1-3 |
|
| k = 2 Steps 1-3 |
|
| k = 3 Steps 1-3 |
|
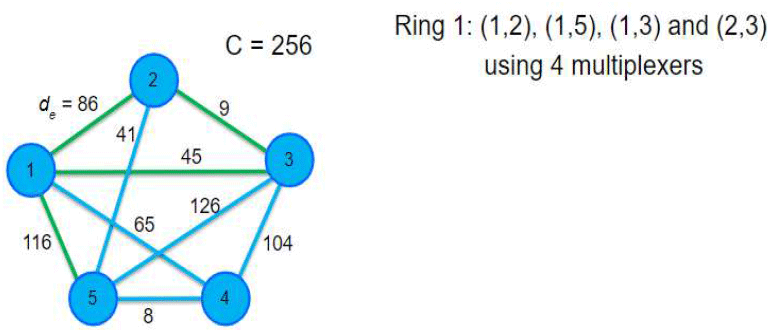
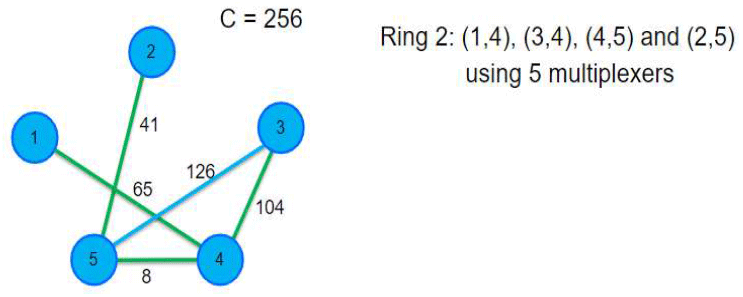
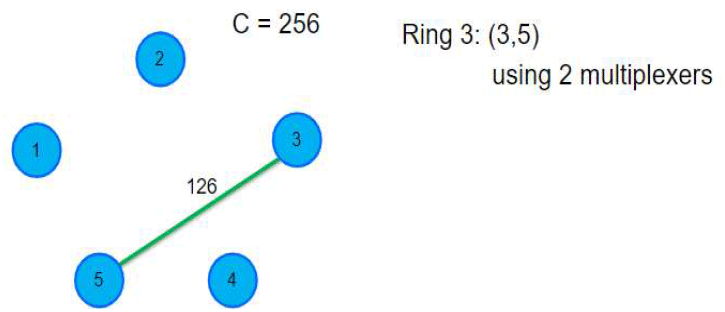
표 1에서 첫 번째 반복단계 (k = 1)에서 초기 선택된 호는 임의의 선택한 호 (1,2)이며, 이 호와 인접한(adjacent) 호 중에서 고리의 잔여용량(C = 256)을 만족하는 가장 큰 용량을 가진 호들인 (1,5)-(1,3)-(2,3)를 순차적으로 첫 번째 고리(Ring 1)에 할당한다. 이때, 마디 1, 2, 3, 4에 각 1개씩 총 4개의 multiplexer가 필요하다. 이후 두 번째 반복단계(k = 2)에서 할당되지 않은 호들 중에서 호(1,4)를 임의로 선택하고, 이어서 다시 순차적으로 호(3,4)-(4,5)-(2,5)를 두 번째 고리(Ring 2)에 추가한다. 마지막 반복단계(k = 3)에서는 잔존하는 유일한 호 (3,5)를 세 번째 고리에 할당하고, 더 이상 남아있는 호가 없으므로 알고리즘을 종료한다. 최종, 그림 6의 네트워크 예제는 모든 호들의 수요를 충족하기 위해서는 고리가 총 3개 요구되며, 각 고리에 호들을 모두 할당하기 위해서는 총 11개(=4+5+2)의 multiplexer가 요구된다는 것을 최종 결과로 얻을 수 있다.
표 1의 결과를 바탕으로, 최적해를 도출해내는 Branch and Cut 알고리즘과 본 논문에서 제시하는 휴리스틱 알고리즘을 각각 적용하여 목적함수 값과 계산시간을 비교하였다. (본 3절에서 제시하는 모든 실험은 Intel Core™ i5-7200U CPU @ 2.50GHz, RAM 8.00GB PC 환경에서 산출된 결과이다.)
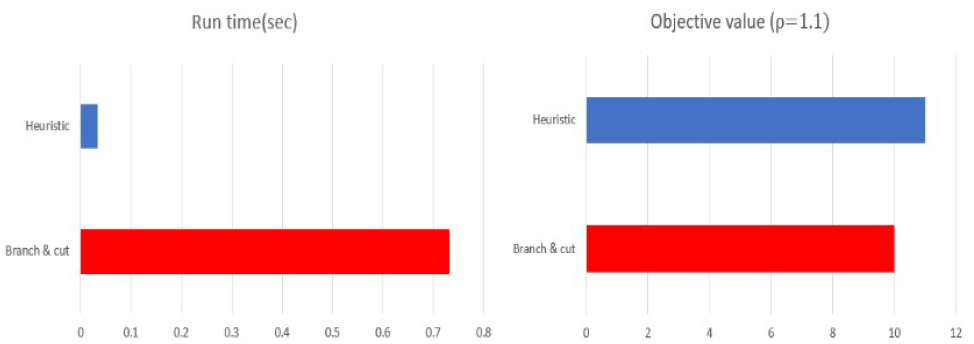
본 논문에서 제안하는 휴리스틱 방법의 계산효율성과 정확도를 분석하기 위해, 정확한 최적해를 도출할 수 있는 Branch & Cut(B&C) 기법을 비교군으로 활용하였다. 표 2는 그림 1의 네트워크 예제를 B&C 기법과 본 논문에서 제안한 GHA를 적용하여 비교한 결과이다. B&C 기법은 MATLAB을 활용하여 스크립트를 작성하였으며, 최적해를 도출하기 위해 GROBI 8.01을 활용하였다. 동일한 예제에 대한 목적함수 값은 각각 10과 11이 도출되였고, GHA를 통해 정확한 최적해를 도출하지는 못하였으나 비교적 근사한 값을 얻었다. 계산시간 면에서는 B&C 기법을 통해 0.7309초, GHA는 0.0341초 만에 결과를 얻음으로써 약 20배 가량 빠른 속도로 보였다.
| exact method (branch & cut) | proposed heuristic (GHA) | |
|---|---|---|
| solving system | GUROBI 8.01/MATLAB | MATLAB 2018a |
| objective value | υopt(I) = 10 | υH(I) = 11 |
| run time | 0.7309 sec | 0.0341 sec |
|
||
본 논문에서 제안하는 GHA의 효용성을 확인하기 위해 추가적인 실험을 진행하였으며, 이때 활용한 파라미터의 값은 표 3과 같다. 고리의 용량(C)은 256이며, 각 호의 수요 de 는 0과 150의 사이 임의의 정수로 선택하였다. 각 문제 예제 별 마디의 수는 4, 5, 6으로 하되, 복잡한 문제 유형 생성을 위해 모든 마디 쌍을 연결하는 호가 존재하는 네트워크(complete network)를 고려하였다.
| capacity of ring (C) | demand of edge de | number of nodes |
|---|---|---|
| 256 | Random integer between (0,150] | 4, 5, or 6 |
표 4에서 보듯이, 각 마디의 수(4, 5, 6)에 대한 문제 예제는 각 10개씩 생성하였으며, 마디의 개수가 4개인 문제 예에서는 최적 목적함수 값의 차이는 +6.85 %로서, GHA가 B&C 기법에 비해 약 6 % 높은 수준의 목적함수 값을 도출하였다. 반면, 계산속도는 B&C 기법에 비해 약 12 배 가량 빨랐다. 마디의 수가 5, 6 개인 문제 예제의 결과를 통해 마디의 수가 많아질수록, 최적 목적함수 값의 개선 정도가 나빠지긴 하지만 그 차이는 점점 감소함을 확인할 수 있었으며, 6 개 마디 문제예제의 경우, B&C 기법에 비해 5,000 배 이상의 빠른 계산속도를 보여주었다. 기존 연구에서 제안되었던 휴리스틱 알고리즘과의 직접적 성능 비교는 제한되나, Sutter et al.(1998)의 연구에서 7개 노드로 구성된 네트워크에 대한 휴리스틱 알고리즘 적용 결과가 계산 시간은 평균 약 4초 정도가 소요되었다.
보다 면밀한 분석을 위해, 마디의 개수가 6개인 10개 문제예제의 결과를 그림 7과 그림 8을 통해 살펴보자.
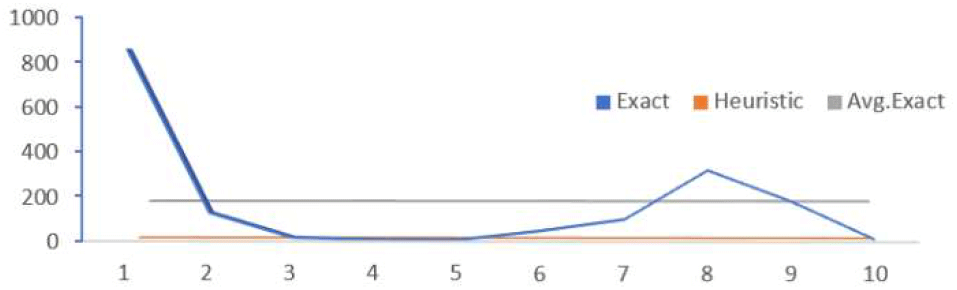
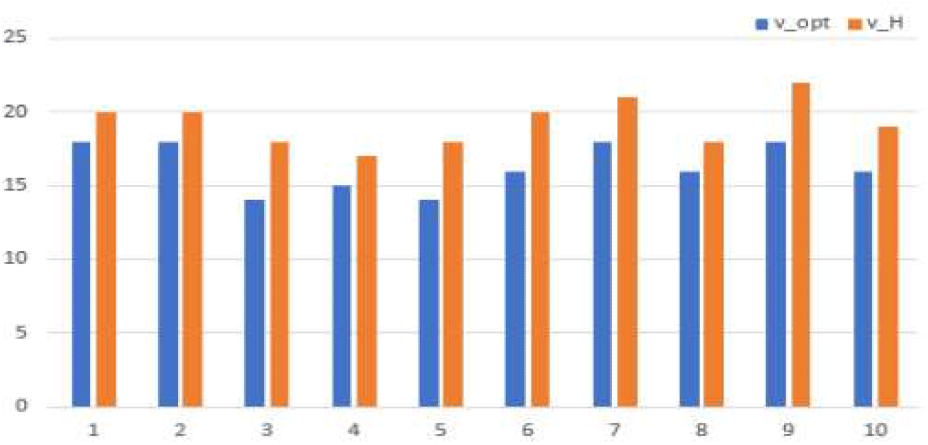
그림 7은 10개 문제 예제에 대한 B&C 기법과 GHA의 계산시간(초)의 결과를 보여준다. GHA의 경우, 모든 문제 예제 대해 계산시간 면에서 큰 차이를 보이지 않는다.(GHA의 계산시간을 표현하는 주황색 선은 상당히 평편한 형상을 보인다.) 하지만, B&C 기법의 경우 문제 예제에 따라 계산시간 면에서 상당히 큰 차이를 보임을 알 수 있다. (문제 예제 #1: 약 861초, 문제 예제 #5: 약 2초)
그림 8은 10개 문제 예제에 대한 B&C 기법과 GHA의 목적함수값 결과를 비교한 것이다. GHA의 경우 모든 문제 예제에 대해 B&C 기법 대비 [2,4] 가량 높은 목적함수 값을 도출해주는 것으로 확인하였다.
4. 결 론
본 논문에서는 현재 육군에서 추진 중인 Army Tiger 4.0 체계의 개념 및 추진방향을 중심으로 향후 드론봇체계 혹은 유·무인 협업체계가 운용되는 작전환경에 적용 가능한 네트워크 multiplexer 할당문제(MAP)에 대해 살펴보았다. 본 모형은 전체 네트워크에 존재하는 호(edge)의 통신 수요를 충족하는 가운데 최소의 multiplexer의 수를 도출해주는 네트워크 최적화 문제이다. 모든 마디 쌍들이 연결된 네트워크에서는 최대 |E|(|E| + |V|)=(|V|4 − |V|2)/4개의 이진변수(binary variables)를 고려해야 하는 복잡한 문제이며, 이론적으로도 짧은 시간 내 최적해를 도출할 수 있는 효율적 알고리즘이 존재하지 않는 것으로 알려져 있다. 실제 전장은 즉응적인 의사결정과 신속한 대응이 필수이므로, 각 상황별 신속하게 대안을 제시해주는 알고리즘의 고안 및 적용이 요구된다. 따라서, Greedy 기반의 휴리스틱 알고리즘을 제안하여, 계산시간상 효율성을 보임으로써 알고리즘의 실제 적용 가능성을 보이고자 하였다.
향후 연구에서는 본 논문에서 제안한 휴리스틱 알고리즘을 발전시켜 해의 정확도를 더욱 향상시킬 수 있을 것으로 기대하며, 기존에 연구된 다양한 휴리스틱 알고리즘과의 정량적 비교 또한 가능할 것이다. 추가적으로 실제 Army TIGER 4.0 체계의 적용과정 0단계(’00년 이후)에 해당하는 사·여단으로 확대 적용하는 과정[2]에서 실제 운용 중인 무인체계 혹은 유·무인 협업체계에 본 네트워크 모형과 해당 해법의 적용함으로써 실제 적용 가능성을 점검해볼 수 있을 것으로 기대된다.