1. 서 론
프로펠러에서 발생한 캐비테이션 소음은 선박 수중방사소음(URN, Underwater radiated noise)의 주요 원인으로 선박의 프로펠러에 침식을 일으킬 뿐만 아니라 해양생태계 피해를 발생시키고 특히 해군 함정의 경우 잠수함에 의한 피탐 가능성을 높이기 때문에 함정의 생존성에 큰 영향을 미친다. 이러한 수중방사소음을 최소화하기 위해 초기 설계 단계부터 프로펠러의 요구성능을 추정하고 공동터널에서 모형 프로펠러 시험을 수행하고 있으며 운용 단계에서는 Prairie System을 운용하고 대잠 상황 시 캐비테이션 초생 속도(CIS, Cavitation Inception Speed) 이하로 기동하는 등 다양한 노력을 기울이고 있다.
캐비테이션은 프로펠러의 회전으로 인해 유체의 압력이 증기압보다 낮아지면서 공동(Cavit)이 발생하는 현상을 말하며 이때 생성된 공동이 붕괴되어 강한 소음과 진동을 발생시키며 프로펠러 표면에 침식을 일으킨다. 캐비테이션은 유체동역학적 현상, 발생 위치, 동적 변화 등의 요인에 따라 다양하게 분류할 수 있으나, 소음관점에서는 프로펠러 날개면에 생성되는 낮은 압력으로 인해 발생하는 얇은층 캐비테이션(Sheet Cavitation)과 날개면 끝 또는 허브에서의 와류꼬임 현상으로 발생하는 날개끝 보텍스 캐비테이션(TVC, Tip Vortex Cavitation) 또는 허브 보텍스 캐비테이션(HVC, Hub Vortex Cavitation)으로 구분할 수 있다.
얇은층 캐비테이션 소음은 프로펠러의 회전운동에 발생하기 때문에 프로펠러의 초당 회전수와 날개 수의 곱으로 산출되는 날개통과주파수(BPF, Blade Passage Frequency)와 관련된 협대역 성분의 주파수 특성을 보이며, 강한 펄스 형태의 소음이 발생하며 프로펠러 상부 선체에 진동을 일으킨다. 반면 보텍스 캐비테이션의 경우 광대역 소음 특성이 있으며 일반적으로 가장 먼저 발생하기 때문에 군사적으로 매우 중요한 소음원으로 간주하고 있다[1].
이러한 캐비테이션의 위치를 추정하기 위한 음향학적 방법에는 빔포밍기법(Beamforming method), 도달시간지연기법(TDOA, Time Difference Of Arrival method) 및 정합장 처리 기법(MFP, Matched Field Processing method)이 있다. 프로펠러 상부 선체에 매립된 센서를 이용하여 캐비테이션 터널에서 실험이 진행되었기 때문에 센서 배치, 터널에 의한 잔향음 등의 제한사항 고려하여 Green 함수를 이용하여 복제음장(Replica pressure field)을 생성하고 실제 계측음장(Measured pressure field)과 유사도를 비교하여 소음원의 위치를 추정하는 정합장 역산 기법을 사용하였다. 정합장 역산 기법의 경우 실험환경을 정확히 반영한다면 매우 정확한 위치 추정이 가능하지만 복제음장을 생성하는데 많은 계산량이 요구된다[2].
김동호 등은 캐비테이션의 발생 여부, 위치 및 세기 등 캐비테이션에 대한 정보를 얻기 위해 프로펠러 상부 선체에 음향 센서를 매립하여 소음을 정합장 처리 기법을 적용하여 초생 캐비테이션의 발생 위치를 추정했다. 제안된 기법은 대형 공동터널에서 수행된 모형시험을 통해 검증되어 캐비테이션 발생 여부 및 초생 보텍스 캐비테이션 위치 추정에 효율적으로 적용할 수 있음을 확인하였다[3].[4].
모형시험에서 사용된 음향 센서는 총 6개이며 음향 센서 수량 감소에 따른 캐비테이션 위치 추정 영향을 검토한 결과 음향 센서 4개까지는 비교적 정확한 위치 추정이 가능했으나 3개의 음향 센서를 이용한 경우 정확도가 현저하게 떨어지는 것을 확인했다. 이는 선체 표면에 매립될 수밖에 없는 음향 센서의 배치상 제약에 기인한 것으로 분석할 수 있으며 이에 따라 깊이 방향의 오차가 크게 나타나는 것을 확인하였다.
따라서 본 연구에서는 순방향 신경망(FNN, Feed-forward Neural Network) 학습 기법을 적용하여 3개의 센서를 이용하고도 기존의 연구보다 정확한 위치 추정을 할 수 있는 모델을 제시하였다. 3개의 센서를 통해 산출된 공분산행렬(CSDM, Cross Spectral Density Matrix)의 원소들을 머신러닝의 입력값으로 사용하고, 6개의 음향 센서를 이용해 계측한 신호를 정합장처리 기법을 적용해 추정한 음원의 위치를 정확한 위치값으로 가정하여 머신러닝의 출력값으로 사용하였다. 학습된 순방향 신경망 모델을 이용하여 캐비테이션 위치를 예측했으며 정합장 역산기법에 의한 위치 추정 결과와 정확도를 비교하였다.
2. 배경 이론
수중에서 잡음의 영향을 최소화하면서 원하는 음향학적 정보를 얻기 위해 센서배열을 이용하는 신호처리기법이 발전되어 왔다. 정합장처리 기법은 센서 배열을 통해 계측된 음장(Measured pressure field)과 음향환경을 반영한 음파전달모델로 얻어진 복제음장(Replica pressure field)간의 유사도 비교를 통해 음전달 특성을 결정짓는 인자들을 도출해내는 역산 문제에 해당한다고 할 수 있다. 따라서 기존의 빔포밍(Beam forming) 기법과는 달리 정확하게 원하는 인자들을 도출할 수 있는 장점이 있지만, 이를 위해 정교한 음파전달모델이 필요하고 전체 공간에 대한 복제음장을 생성해야 하므로 많은 계산시간이 요구된다는 제약점이 있다. 이러한 제약점을 극복하고 보다 효율적인 해를 찾기 위해 최적화 기법이 적용되었으며, 이러한 방법을 정합장 역산 기법(Matched-field inversion method)이라고 한다.
이때 2개 이상의 주파수에서 복제 음장과 계측 음장의 유사도를 비교하여 유사도가 가장 높은 역산 인자를 도출하는 것을 광대역(Broadband) 정합장 역산 기법이라고 한다[5][6]. 가장 널리 사용되는 정합장 프로세서는 Bartlett 프로세서로 계측신호 벡터 “P”와 복제음장 벡터 “R”간의 내적의 형태로 구성된다.
계측음장과 복제음장 간 상관도를 직접 평가하는 Bartlett 프로세서를 이용하여 최소화하고자 하는 목적함수 “E(Φ)”를 식 (1)과 같이 정의하고 목적함수가 최소화되는 역산 인자(Φ(x,y,z))가 소음원의 위치가 된다. 여기에서 위첨자 H는 Hermitian 연산자를 의미한다.
광대역 프로세서는 각 주파수에서의 프로세서 출력값에 대한 비상관 평균(Incoherent average)을 취하는 형태로 식 (2)와 같이 정의될 수 있다. 이때, Nf는 역산에 사용된 주파수의 수를 의미한다.
식 (1)에서 “”은 식 (3)과 같이 정의되며 “i”번째 주파수에 대한 정규화된 공분산행렬(CSDM, normalized Cross Spectral Density Martrix)을 의미한다.
여기서 “Pl”은 주파수 “fi”에서 계측신호의 “l”번째 Snapshot 벡터를, “L”은 Snapshot의 수를 나타낸다. 본 연구에서는 20~70kHz 대역통과 필터 처리된 시계열 신호에서 나타난 피크 신호를 데이터로 매우 짧은 신호를 사용하였기 때문에 단일 스냅샷(Single snapshot)에 의한 광대역 정합장 역산 기법을 적용하였다. 또한, 6개의 센서를 모두 이용하여 정합장 처리해 추정한 음원의 위치가 정확한 캐비테이션 위치로 가정하여 순방향 신경망 모델 학습을 위한 목표값(Target value)으로 사용하였다.
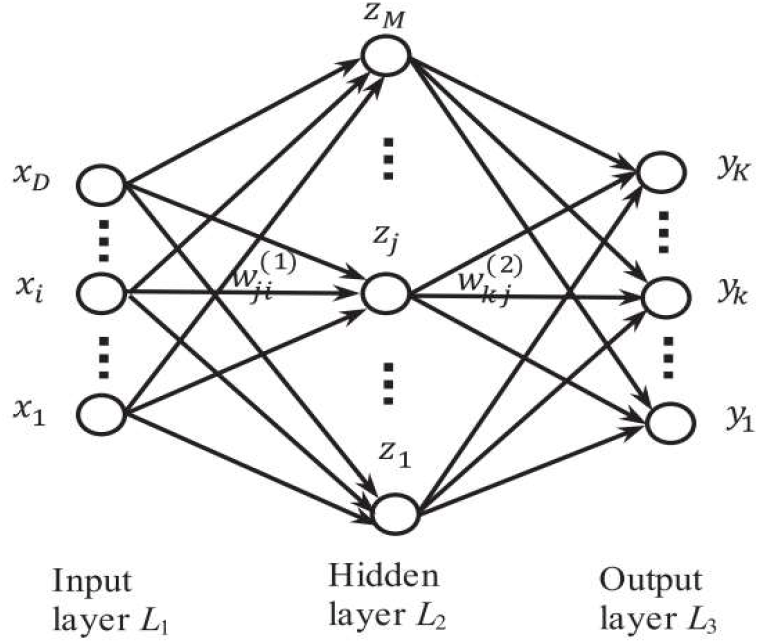
다층 퍼셉트론 신경망(Multi-layer perceptron neural network)이라고도 알려진 순방향 신경망(FNN, Feed-forward Neural Network)은 그림 1과 같이 순방향의 비순환 신경망 구조를 사용한다. 출력값(Output)은 식 (4)와 같이 입력값(Input)와 가중치(Weight)의 함수에 의해 결정된다[7]. 순방향 신경망 구조는 3개의 계층으로 입력층(Input layer, L1), 은닉층(Hidden layer, L2), 출력층(Output layer, L3)로 구성되어 있으며 입력층 “L1”은 “D”개의 입력 변수로 구성되며 “X=[x1,…,xD]T”로 구성된다. 입력 함수의 선형 결합에 의한 “j”번째 값은 아래 식 (4)와 같이 표현할 수 있다.
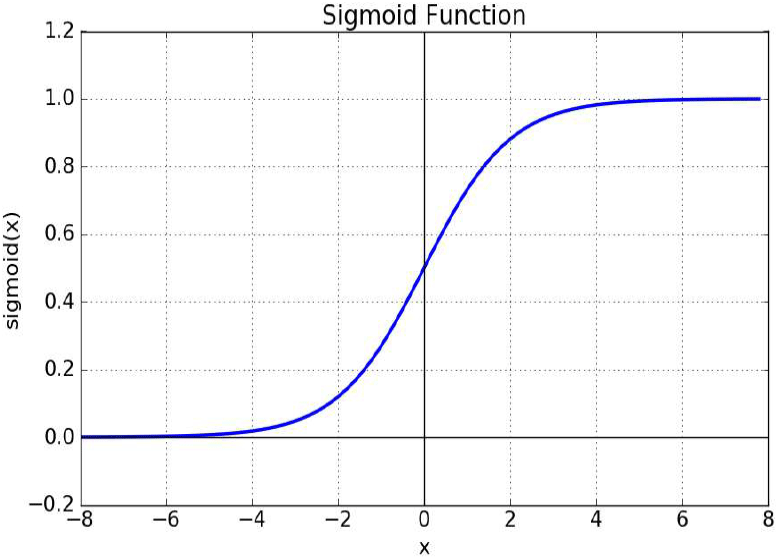
여기에서 “M”은 은닉계층 “L2”에서 뉴런의 수를 의미하며 매개변수 “”와 “”은 각각 가중치(Weight)와 편향(Bias)을 의미한다. 은닉계층에서는 그림 1.(b)와 같이 시그모이드 함수를 사용하여 활성화하며 아래 식 (5)와 같다.
이와 유사하게 출력층 “L3”에서 “K”개의 출력값의 활성화 함수는 은닉계층의 “zj”값을 선형 결합으로 식 (6)과 같이 나타낼 수 있다. 여기에서 매개변수 “”와 “”는 각각 2번째 계층의 가중치와 편향을 의미한다.
이때, 출력값이 이산화된 값을 갖거나 레이블(Label)이 지정된 값을 출력하는 경우 분류(Classification) 문제에 해당하며 출력값이 연속적인 값을 갖는 경우 회귀(Regression) 문제에 해당한다.
회귀 문제의 경우, 출력값 “yk”는 항등함수를 사용하여 마지막 계층에서 출력된 값과 동일한 값을 갖는다.반면 다중 클래스 분류 문제의 경우 일반적으로 출력층에서 소프트맥스(Softmax) 함수를 활성화 함수로 사용한다. 출력값 “yk”은 아래 식 (7)과 같이 나타낼 수 있다.
“W”는 모든 가중치와 편향값으로 이루어지며 출력값은 “0≤yk≤1”, “∑kyk=1”을 만족한다. 분류 및 회귀 문제에서 가중치와 편향값은 식 (8)과 같이 순방향 신경망 모델의 훈련 데이터(Training data)의 목표값 “yk target (X)”과 신경망에 의한 출력값 “yk (X,W)”의 오차가 최소화되도록 최적화 과정 수행을 통해 도출된다.
여기에서 “g(•)”는 최적화 알고리즘을 의미하며 분류 문제에서는 쿨백-라이블러 발산(Kullback-Leibler Deivergence), 회귀 문제에서는 르젠버그-마크워트(Levenberg-Marquardt), 베이즈 정규화(Bayesian regularization), 스케일링 된 켤레 기울기(Scaled conjugate gradient) 등이 사용된다.
본 연구는 캐비테이션의 위치를 연속적인 값으로 가정하여 회귀 학습모델을 사용하였다. 순방향 신경망 훈련을 위해 사용한 데이터의 입력값은 3개의 음향 센서를 이용하여 광대역 정합장 처리에 사용되는 공분산행렬(CSDM) 생성하고 그 원소들을 사용하였다. 목표값은 6개의 음향 센서를 사용하여 정합장 역산 기법을 통해 추정한 음원의 위치를 사용하였다. 다양한 최적화 알고리즘을 이용하여 훈련을 수행하였으며 CPU 처리 시간, 위치 추정 성능 등을 고려하여 최적의 알고리즘을 선정하였다.
3. 실험결과
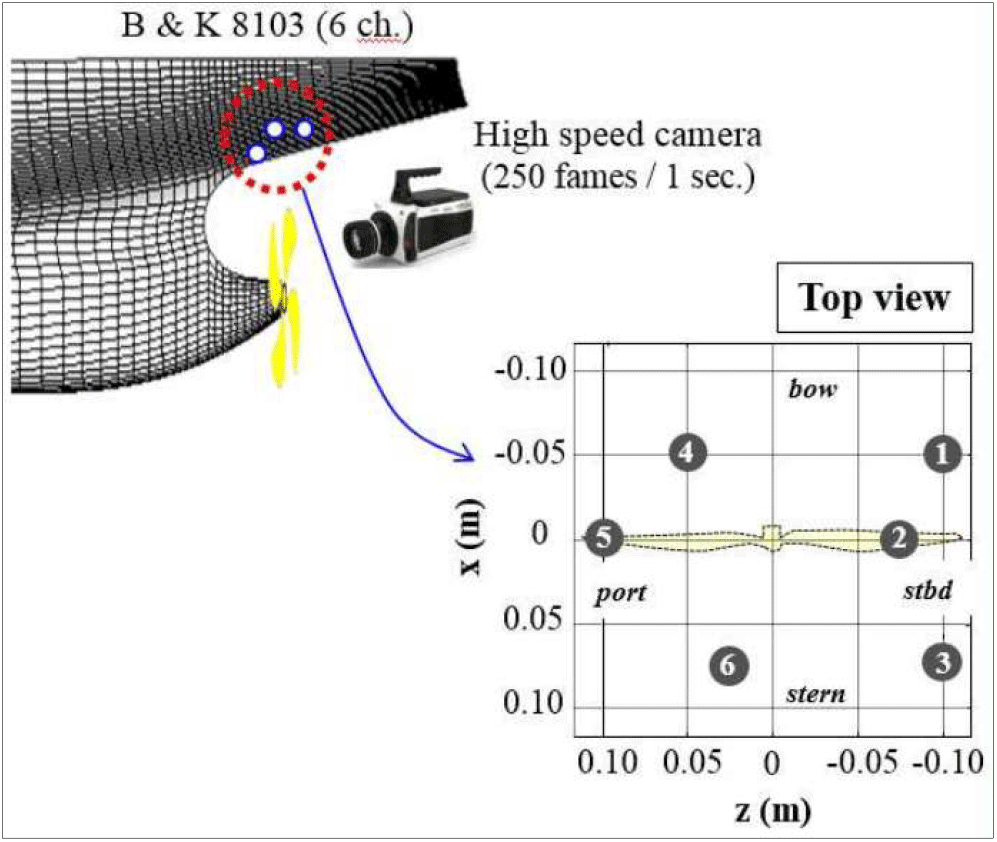
본 연구에 활용한 데이터는 모형선을 이용하여 삼성공동터널에서 진행한 초생캐비테이션 발생 실험 데이터를 사용하였다. 날개가 4개인 프로펠러가 장착된 모형선을 이용하였으며, 총 6개의 B&K8103 센서를 프로펠러 상단 선체에 그림 3과 같이 프로펠러 상부에 매립하였다. 터널내의 유속은 4m/s로 유지하였으며, 용존 산소량은 75%로 유지하였다. 프로펠러의 회전수는 1390rpm으로 고정시킨 상태에서 터널 내부 압력을 비공동 상황에서 서서히 감압하여 서서히 보텍스 캐비테이션을 발생시키는 방식으로 실험을 진행하였다. 센서의 샘플링 주파수 256kHz로 총 10초 동안 음향신호를 계측하였으며, 이때 발생된 캐비테이션의 형상을 관찰하였다. 세부적인 실험 조건 및 시각적으로 관찰된 날개에서의 캐비테이션 형상은 각각 표 1, 그림 4와 같다.

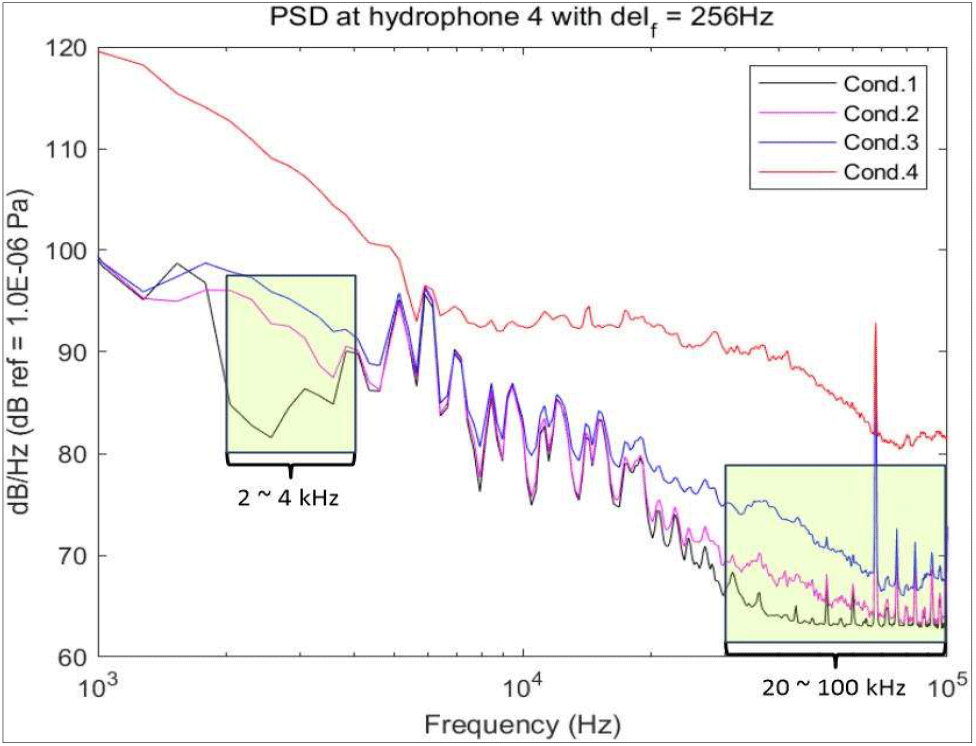
Test Cond.1은 비공동 상황으로 캐비테이션이 관측되지 않았으며, Test Cond.2는 육안으로는 캐비테이션이 관측되지 않았으나 그림 5의 파워스펙트럼 밀도를 보면 2 ~ 4 kHz 영역에서 약 10 dB, 20 ~ 100 kHz 영역에서 약 2 ~ 3 dB가 증가함을 확인할 수 있었다. Test Cond.3의 경우 그림 4(b)와 같이 매우 간헐적으로 프로펠러 상사점(TDC) 부근에서 보텍스 캐비테이션이 발생하는 것이 관측되었으며, 해당 파워스펙트럼 또한, 2 ~ 4 kHz, 20 ~ 100 kHz 영역에서 10 dB 이상 증가함을 확인할 수 있다. 이때 보텍스 캐비테이션은 날개 끝단에서부터 생성되지 않고, 날개가 상사점을 지나간 다음에 불규칙적으로 생성되었다.
보텍스 캐비테이션은 길게 늘어지지 않고 매우 짧게 생성되었다가 바로 사라지는 경향을 보였다. Test Cond.4는 그림 4 (c-1, c-2)와 같이 두 가지 형태의 캐비테이션이 관측되었으며, 전 주파수 영역에서 파워스펙트럼 밀도가 증가하였다. 첫 번째 형태(그림 4(c-2))는 날개가 상사점 부근을 지나갈 때마다 생성되는 길게 늘어진 형태의 보텍스 캐비테이션으로 프로펠러가 상사점 위치에 도착했을 때 날개 끝단에서 시작하여 우현으로 발달된 후 소멸되었다. 다른 형태(그림 4(c-1))는 간헐적으로 발견되는 Test Cond.3와 같은 형태의 캐비테이션이었다.
본 절에서는 순방향 신경망을 이용한 캐비테이션 예측 모델을 생성하기 위해 훈련에 필요한 데이터를 생성하기 위해 주파수 대역선정, 신호단편 데이터 생성, 데이터 전처리 및 훈련 과정에 관해 기술하였다.
캐비테이션의 발생 위치 추정을 위한 주파수 대역은 그림 5의 파워스펙트럼 밀도에서 캐비테이션 발달에 따라 파워스펙트럼 밀도가 증가하는 20 ~ 70 kHz 영역을 관심 주파수 대역으로 선정하였으며, 70 kHz 이상은 전기잡음으로 추정되는 협대역 잡음 신호들이 존재하여 관심 주파수 대역에서 제외하였다.
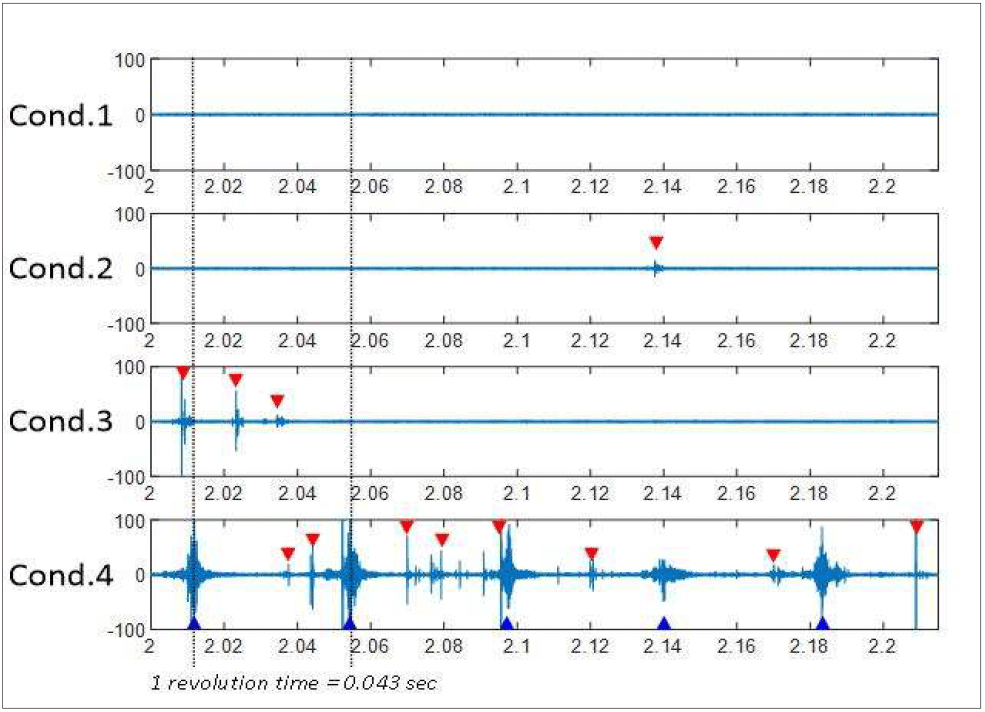
선정된 주파수 대역과 캐비테이션과의 연관성을 확인하기 위하여 Test Cond.1 ~ 4의 시계열 신호를 대역통과 필터(Bandpass filter)를 적용시켜 공동수 변화에 따른 신호의 변화를 오른쪽 그림 6과 같이 관찰하였다.
 )/Chirp(
)/Chirp( ) 신호 발생 패턴 | Result of bandpass filtered signals and the pattern of Pop(
) 신호 발생 패턴 | Result of bandpass filtered signals and the pattern of Pop( )/Chirp(
)/Chirp( ) signal
) signal
그림 6을 살펴보면 Test Cond.1에서는 신호 변화가 관찰되지 않아 비공동 상황임을 확인하였다. Test Cond.2의 경우 시각적으로는 캐비테이션이 관찰되지 않았으나, 음향신호에는 불규칙적이고 간헐적인 Pop 형태의 신호(▼)가 발견되었으며 이는 시각화되기 이전에 발생하는 매우 작은 크기의 캐비테이션으로 인한 소음으로 예측하였으며 Test Cond.3의 경우 큰 진폭의 Pop 형태의 신호(▼)를 확인하였으며 그림 4(b)와 같이 매우 짧은 시간동안 발생하고 사라지는 캐비테이션의 소음에 기인한 것으로 판단하였다[2].
Test Cond.4는 프로펠러 회전 주기(0.043 초)에 따라 Chirp 형태의 신호( )가 발생하는 확인할 수 있었고 이와 동시에 간헐적으로 Pop 형태의 신호(
)가 발생하는 확인할 수 있었고 이와 동시에 간헐적으로 Pop 형태의 신호( )도 발생하였다.
)도 발생하였다.
이러한 관심 주파수 영역으로 대역통과된 신호 분석을 통해 20 ~ 70 kHz 주파수 영역이 캐비테이션 현상과 밀접하게 관련된 주파수 영역임을 확인하였으며 선정된 주파수 영역을 1 kHz 간격으로 총 51개의 주파수를 활용하여 광대역 정합장 역산 기법에 활용하였다.
대역통과 필터를 적용한 신호에서 Pop 또는 Chirp 형태와 같은 피크(Peak) 신호를 관찰하였고 이러한 신호는 캐비테이션에 기인하는 것으로 분석하였다. 본 연구에서는 각각의 피크 신호가 발생하는 지점에서 캐비테이션 발생 위치를 추정하기 위하여 그림 7과 같이 피크 신호가 발생하는 지점을 기준으로 0.015초 (4096 point)의 짧은 시간 구간의 신호를 검출하여 순방향 신경망 훈련에 필요한 시계열 데이터를 생성하였다.
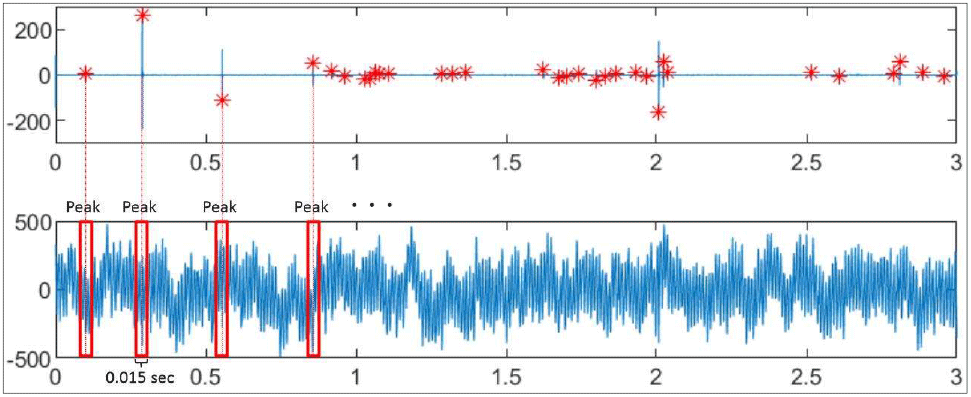
위와 같은 방법으로 전체 10초 길이의 시계열 신호에서 각 실험 신호별 피크 신호를 검출한 결과 비공동 상황인 Test Cond.1에서는 피크 신호가 검출되지 않았으며, Test Cond.2에서 Pop 신호 23개, Test Cond.3에서 Pop 163개, Test Cond.4에서 Chirp 신호 231개를 검출하여 총 417개(N)의 데이터를 검출하여 신호단편 데이터를 생성하였으며 각 데이터에는 총 6개 음향 센서에서 계측 신호가 포함되어 있다.
순방향 신경망 모델 훈련을 위한 입력값은 3개(S)의 음향 센서 데이터를 이용한 공분산행렬(CSDM)의 원소로 구성된다. 총 6개 중 3개의 음향 센서를 조합하여 공분산행렬을 생성하는데 기존의 연구[2]를 통해 캐비테이션 발생 위치와 가장 근접한 2번 센서를 포함하여 센서를 조합한 경우 위치 추정 정확도가 향상되는 것을 확인하였다. 따라서 본 연구에서도 2번 센서를 포함한 3개의 센서 조합, 총 10개의(C) 조합을 사용하여 총 4,170가지 경우(N×C)에 대한 공분산행렬 값을 계산하였다.
식 (3)에 따라 생성된 공분산행렬은 3×3 크기를 가지며 식 “”와 같은 특징을 갖는 에르미트 행렬(Hermitian matrix)이다. 따라서 그림 8과 같이 행렬의 상부 삼각 부분의 원소(Upper triangular element)를 실수부와 허수부로 분리하여 12개(S×(S+1))의 값을 벡터화하였다. 동일한 방법으로 선정된 51개(F)의 주파수에 대한 각각의 공분산행렬 원소를 구하면 각 데이터는 총 612개의 입력 변수를 갖는다.
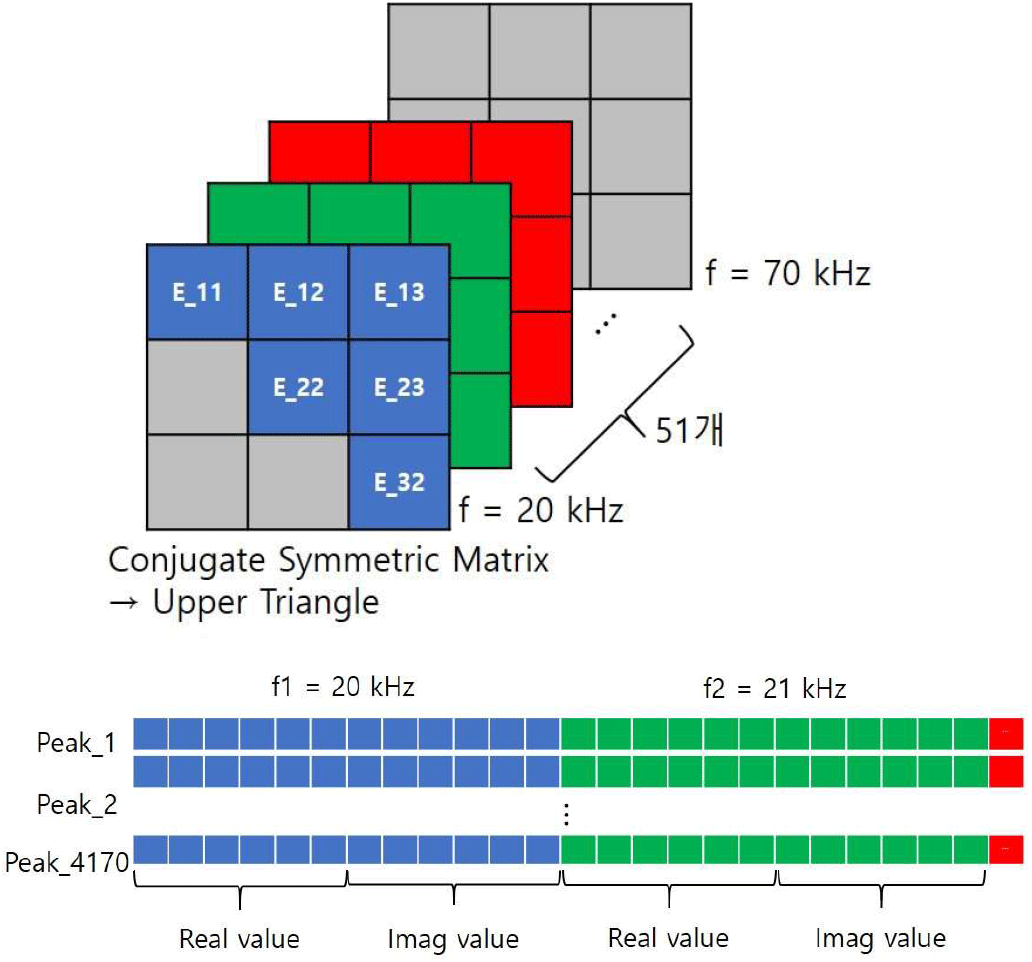
목표값은 6개의 센서를 정합장 역산 기법을 통해 추정된 역산 인자인 음원 위치의 x, y, z 좌표 3개이며 각각의 피크 신호단편 총 4,170개에 대해 동일한 과정을 반복하였다.
주파수 대역 선정 및 신호단편 데이터 생성, 데이터 전처리 과정을 통해 만들어진 4,170개의 데이터는 훈련 데이터(Training data) 60%, 검증 데이터(Validation data) 20%, 시험 데이터(Test data)로 무작위로 분할하여 순방향 신경망 모델 훈련을 수행하였다.
과적합(Over-fitting) 방지 및 CPU 처리 시간 등을 고려하여 은닉계층(Hidden Layer)는 5개로 설정하였으며 최적화 알고리즘은 회귀 훈련에 사용되는 르젠버그-마크워트(Levenberg-Marquardt)[9], 베이즈 정규화(Bayesian Regularization)[10], 스케일링된 켤레기울기(Scaled Conjugate Gradient)[11] 등 3종류의 최적화 알고리즘을 각각 3회 사용하여 비교하였다. 훈련 결과 표 2와 같은 결과를 얻었으며 CPU 처리 시간 및 위치 추정 성능을 고려하여 르젠버그-마크워트 알고리즘을 순방향 신경망 모델 훈련에 사용하였다.
| RMSE [m] | ||
|---|---|---|
| 3 Sensor_MFP | 3 Sensor_FNN | |
| x_position | 0.0779 | 0.0442 |
| y_position | 0.1206 | 0.0738 |
| z_position | 0.0730 | 0.0410 |
| Distance | 0.1611 | 0.0953 |
신호처리 및 순방향 신경망 훈련 및 시험에 사용된 상용프로그램은 Mathworks 社의 MATLAB을 사용하였으며 사용된 프로세서는 Intel(R) Core i5-8500 CPU @ 3.00 GHz, 16 GB RAM을 사용하였다.
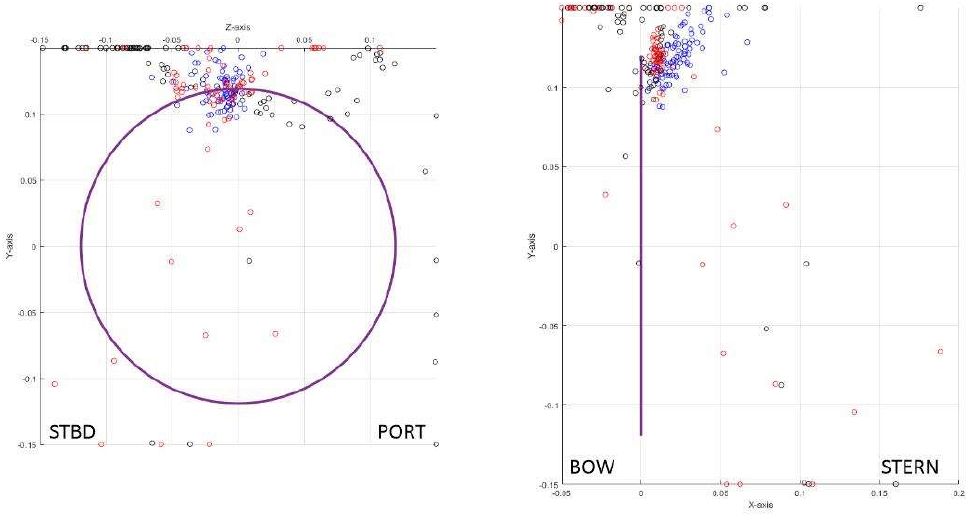
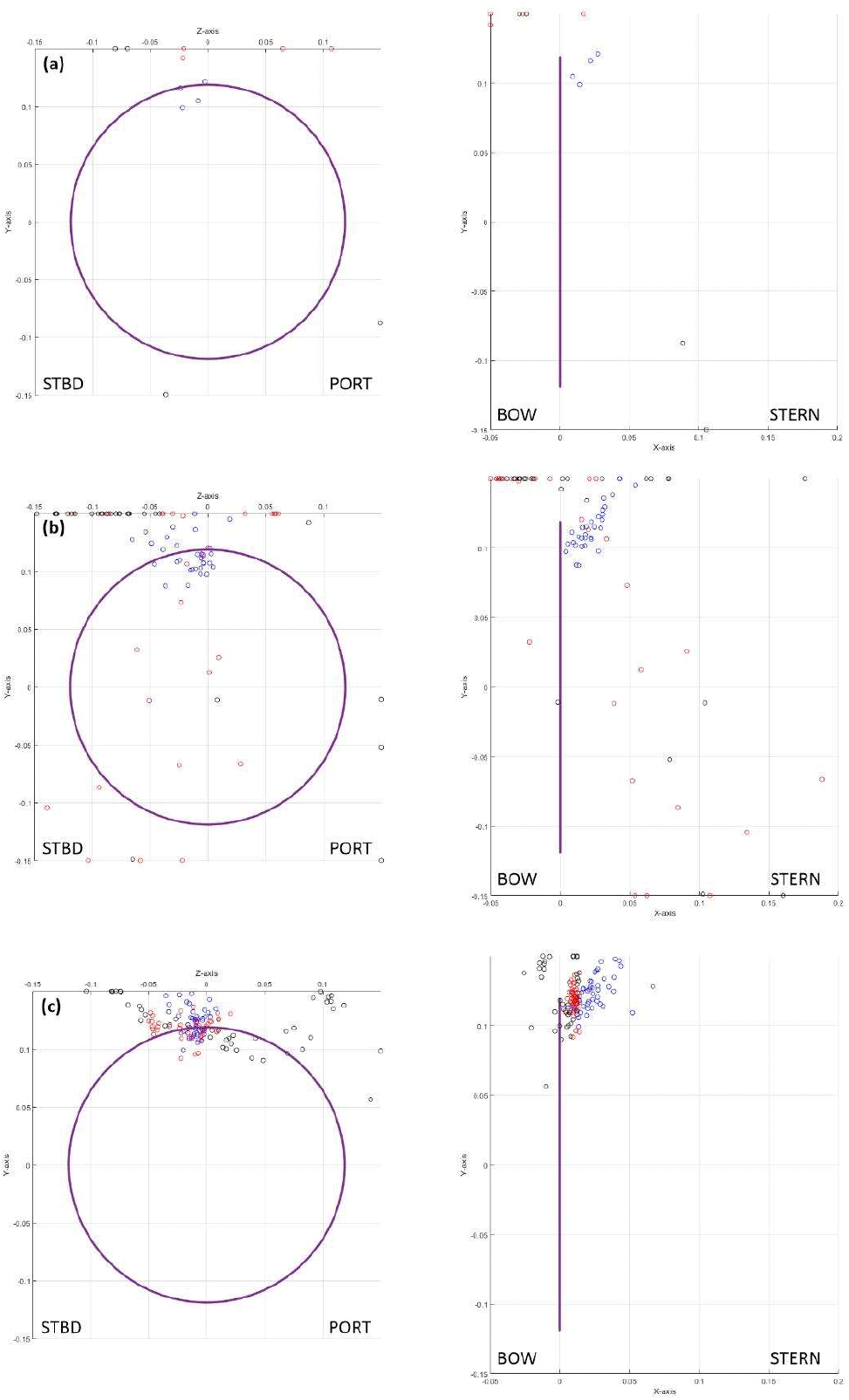
순방향 신경망 모델을 시험 데이터(Test data)에 적용하여 예측한 음원의 위치와 3개의 음향 센서로 정합장 역산 기법을 이용해 추정한 음원의 위치를 정확하다고 가정한 음원의 위치를 기준으로 평균제곱근 오차(RSME, Root Mean Square Error)를 비교하여 표 3과 같이 나타내었다. 전체 Test Cond에서 피크 신호의 위치 추정 결과를 프로펠러 회전평면에 도시한 결과는 그림 9와 같으며 Test 조건별 위치 추정 결과는 그림 10과 같이 나타났다.
 ), 3 Sensor_FNN(
), 3 Sensor_FNN( ), 6 Sensor_MFP(O))
), 6 Sensor_MFP(O))
 ), 3 Sensor_FNN(
), 3 Sensor_FNN( ), 6 Sensor_MFP(O))
), 6 Sensor_MFP(O))
표 3을 통해 순방향 신경망 모델을 이용하여 음원의 위치를 예측한 경우 평균제곱근 오차(RMSE)가 매우 작게 나타나는 것을 확인할 수 있고 그림 9을 통해 프로펠러 회전 평면에 도시한 결과 순방향 신경망 모델을 통해 예측한 음원의 위치(O)가 정확할 것으로 가정한 6개의 음향 센서로 정합창 처리해 얻은 음원의 위치(O)에 근접하여 군집되어 있음을 확인하였다.
그림 10을 통해 모든 실험 조건에서 순방향 신경망 모델을 활용한 경우 위치 추정 성능이 향상되는 것을 확인할 수 있다. 또한, Test Cond.4에서 Chirp 형태의 피크 신호를 이용하여 위치를 예측한 값이 정확도가 높았으며 Test Cond.2~3의 Pop 형태의 피크 신호를 이용한 경우 비교적 정확도가 낮음을 확인할 수 있다.
방향 신경망 학습의 목표값으로 설정했던 6개의 센서로 정합장 처리하여 얻은 음원의 위치는 실제 캐비테이션의 위치임을 확인할 수 없다. 특히 매우 짧은 0.015초 시간의 피크신호를 사용하였기 때문에 위치 추정에 단일 스탭샷을 사용하였다.
본 연구의 한계점으로는 정확한 음원의 위치로 가정하여 순방향 신경망 학습의 목표값으로 설정했던 6개의 센서로 정합장 처리하여 얻은 음원의 위치는 실제 캐비테이션의 위치임을 확인할 수 없다. 특히 매우 짧은 0.015초 시간의 피크신호를 사용하였기 때문에 위치 추정에 단일 스탭샷을 사용하였다. 이는 기존의 연구에서 10초 길이의 신호에서 다중 스냅샷을 이용해 캐비테이션의 위치를 추정했을 때 그 위치가 프로펠러의 우측 상부인 것을 고려할 때 짧은 신호를 사용한 경우에는 프로펠러 면에 퍼져 있는 것을 확인할 수 있었다.
4. 결 론
본 연구에서는 모형선 선체에 매립된 음향센서를 이용하여 프로펠러 캐비테이션 발생 여부, 발생 위치를 추정하는 기존의 방법에 순방향 신경망이라는 머신러닝 모델을 적용하여 필요한 센서 수량을 감소시키면서 음원의 위치 추정 성능을 향상시키는 기법을 제시하였다.
머신러닝 예측 모델을 적용한 결과 기존의 연구를 통해 확인한 캐비테이션 발생 위치와 유사함을 확인하여 순방향 신경망 모델을 이용한 소음원 위치 추정 기법이 유효함을 확인하였다. 이를 통해 최소한 4개 이상의 센서 배열에서 정확한 위치추정이 가능했던 기존의 방법을 3개의 센서만을 이용하고도 음원 위치 추정이 가능했다. 이러한 기법을 통해 캐비테이션 발생 여부 및 발생 위치 추정을 위해 필요한 선체 매립 센서의 수량을 줄임으로써 관측창을 대체하여 캐비테이션 실시간 감시 기술을 실선에 적용하는데 있어서 필요한 노력과 비용을 절감할 수 있을 것으로 기대한다.
향후 본 연구에서 단일 스냅샷에 의한 낮은 해상도에서 기인한 목표값의 오차를 보정하고 고속카메라에서 관찰되는 실제 캐비테이션 위치와의 비교 등을 통해 더욱 정확한 인공신경망을 활용한 예측 모델을 만들 수 있을 것으로 기대되며 더 나아가 실시간으로 캐비테이션 발생 위치를 추정하여 선박에서 발생하는 수중방사소음을 적극적으로 통제할 수 있는 기술로 발전할 수 있을 것이다.